Už jste někdy zkusili hru zvanou curling? Při ní posíláte po ledě žulový kámen o hmotnosti skoro 20 kg do středu kruhů vzdálených více než 40 m. Curlingový kámen se na začátku pohybuje rychlostí o velikosti 2,6 m/s (viz obrázek). Jaké síly na něj působí?

Zdroj
Pokud budeme uvažovat pouze kolmou tlakovou sílu a tíhovou sílu (viz obrázek), které jsou stejně velké a opačně orientované, výsledná síla působící na kámen bude nulová a kámen se bude pohybovat rovnoměrným přímočarým pohybem (1. Newtonův zákon).
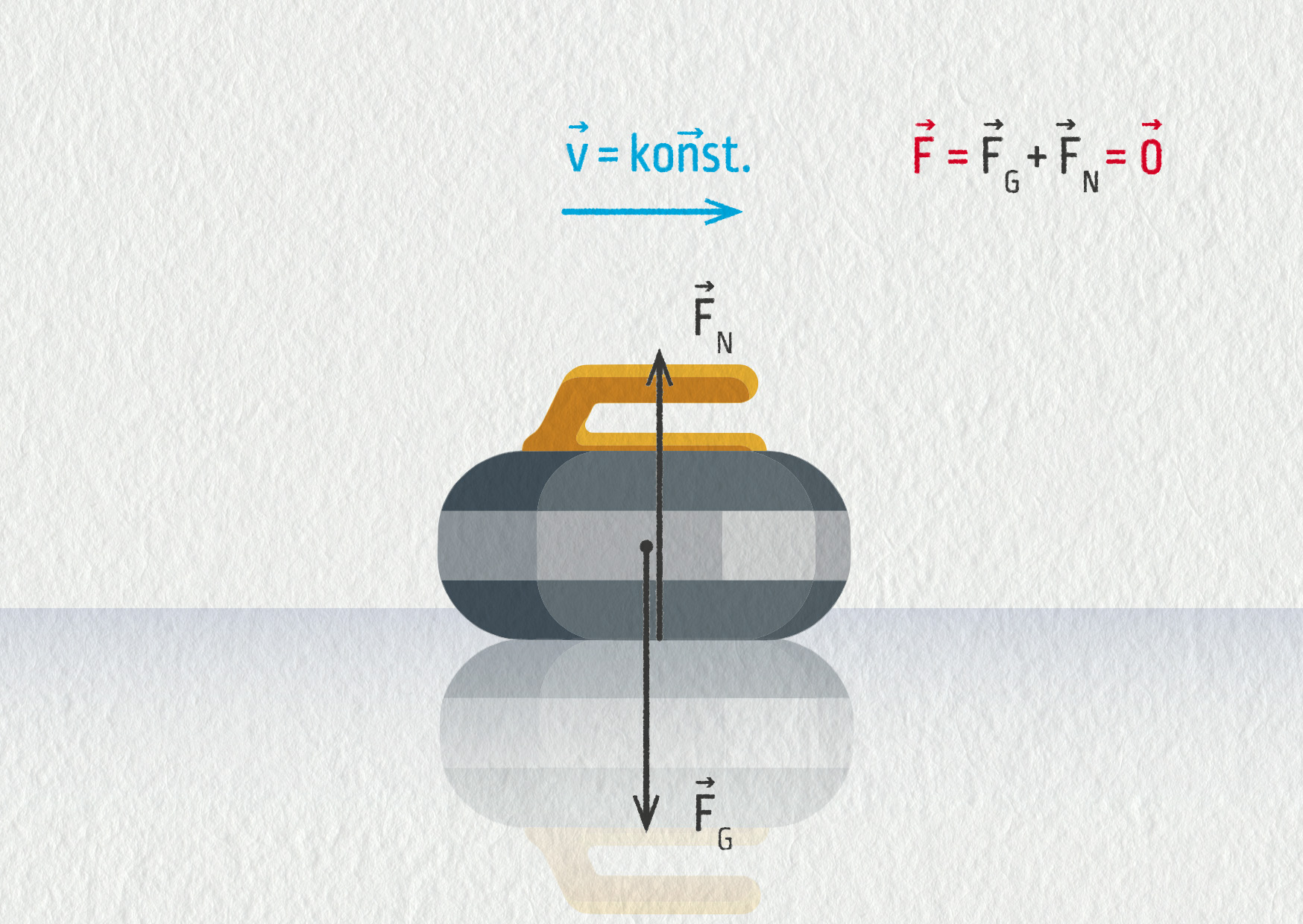
Zdroj
To však hra nebude možná. Cílem je umístit kámen do protějších kruhů. Kámen tedy musí zastavit. Musí na něj působit malá třecí síla mezi kamenem a ledem, a ačkoliv se kolmá tlaková síla a tíhová síla vyruší, proti třecí síle již žádná síla nepůsobí. Výslednice sil tedy působí proti směru pohybu a kámen zpomaluje.
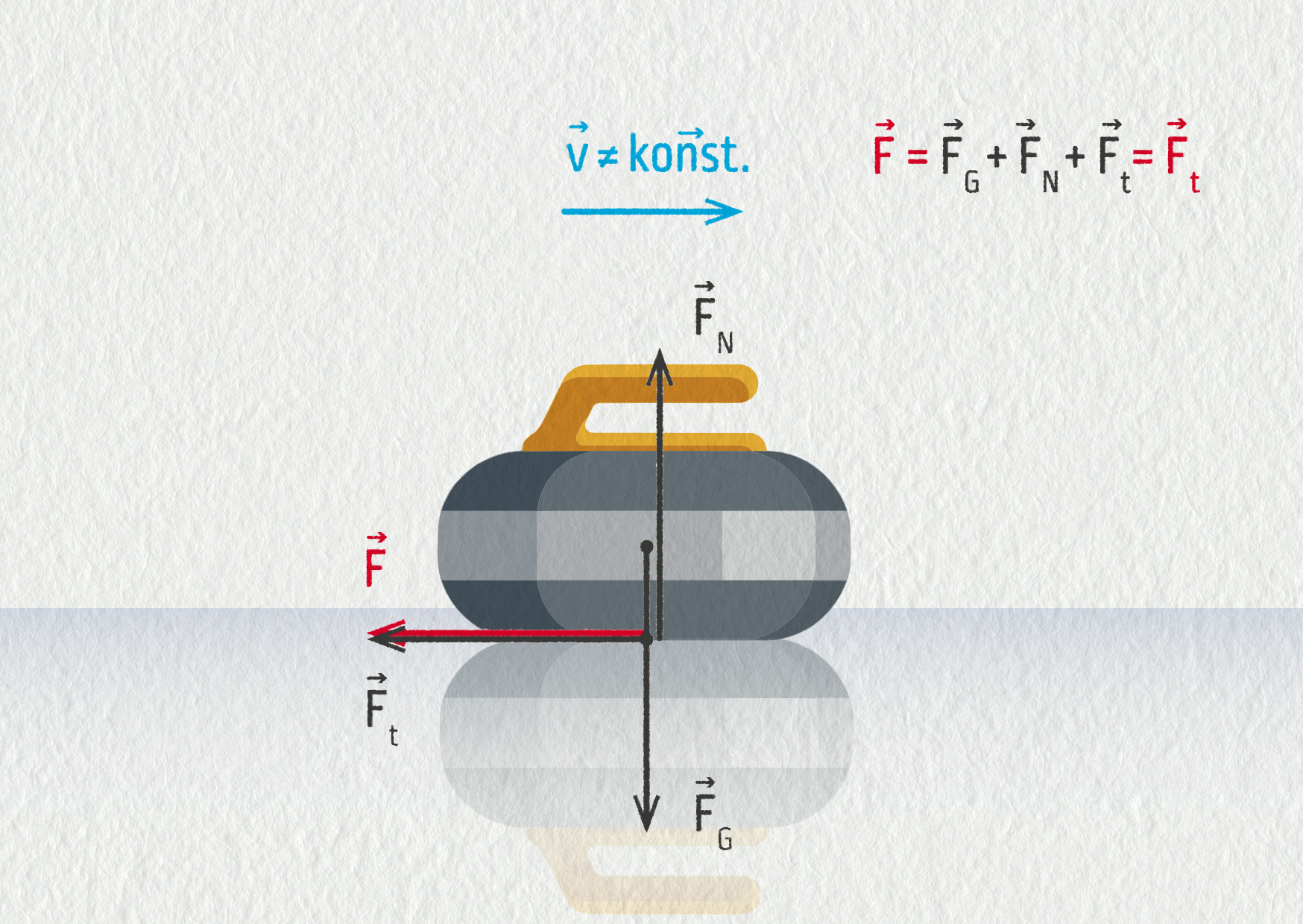
Zdroj
Jak jsme viděli v předchozím příkladu, vlivem tření mezi ledem a kamenem se jeho pohyb zpomalí tak, že se nakonec zastaví v kruzích na opačném konci curlingové dráhy. Jinak by hra nebyla možná. V případě nenulové výsledné síly působící na těleso se bude měnit rychlost pohybu. To je vyjádřením zákona síly – 2. Newtonova zákona.
Formulovat zákon síly přesněji nám umožní pokus s vozíkem, který si můžete vyzkoušet v rámci laboratorních cvičení. V průběhu tohoto experimentu se snažíme působit na vozík na kolejnicích konstantní silou a pomocí sonaru měřit jeho zrychlení.

Zdroj
Těmito pokusy dojdeme k závěru, že pro velikost zrychlení vozíku platí \(a=F/m\). A to je matematické vyjádření druhého Newtonova zákona.
Zrychlení tělesa \(\Vec{a}\) je přímo úměrné výsledné působící síle \(\Vec{F}\) a nepřímo úměrné hmotnosti tělesa \(m\):
\[\Vec{a}=\frac{\Vec{F}}{m}\quad\]nebo také
\[ \quad\Vec{F}=m\Vec{a}\]Setkáme se také s vyjádřením ve tvaru \[\sum_i \Vec{F}_i = m\Vec{a}\;,\] který připomíná, že výsledná síla vzniká jako součet všech vnějších sil působících na těleso.
Vztah jsme zapsali pomocí vektorů. To znamená, že směr zrychlení je vždy stejný jako směr výsledné síly. Jestliže bylo těleso původně v klidu (jako v našem pokusu s vozíkem), zrychluje ve směru působící síly. Rozhodně ale neplatí, že rychlost tělesa má vždy stejný směr jako výsledná síla. Tady vstupuje do hry ještě počáteční rychlost tělesa. Zkuste si představit třeba tenisový míček vyhozený do vzduchu (viz obrázek). Tíhová síla po celou dobu pohybu působí směrem dolů. Stejný směr má tedy i zrychlení a toto platí pro výstup i pád míčku.
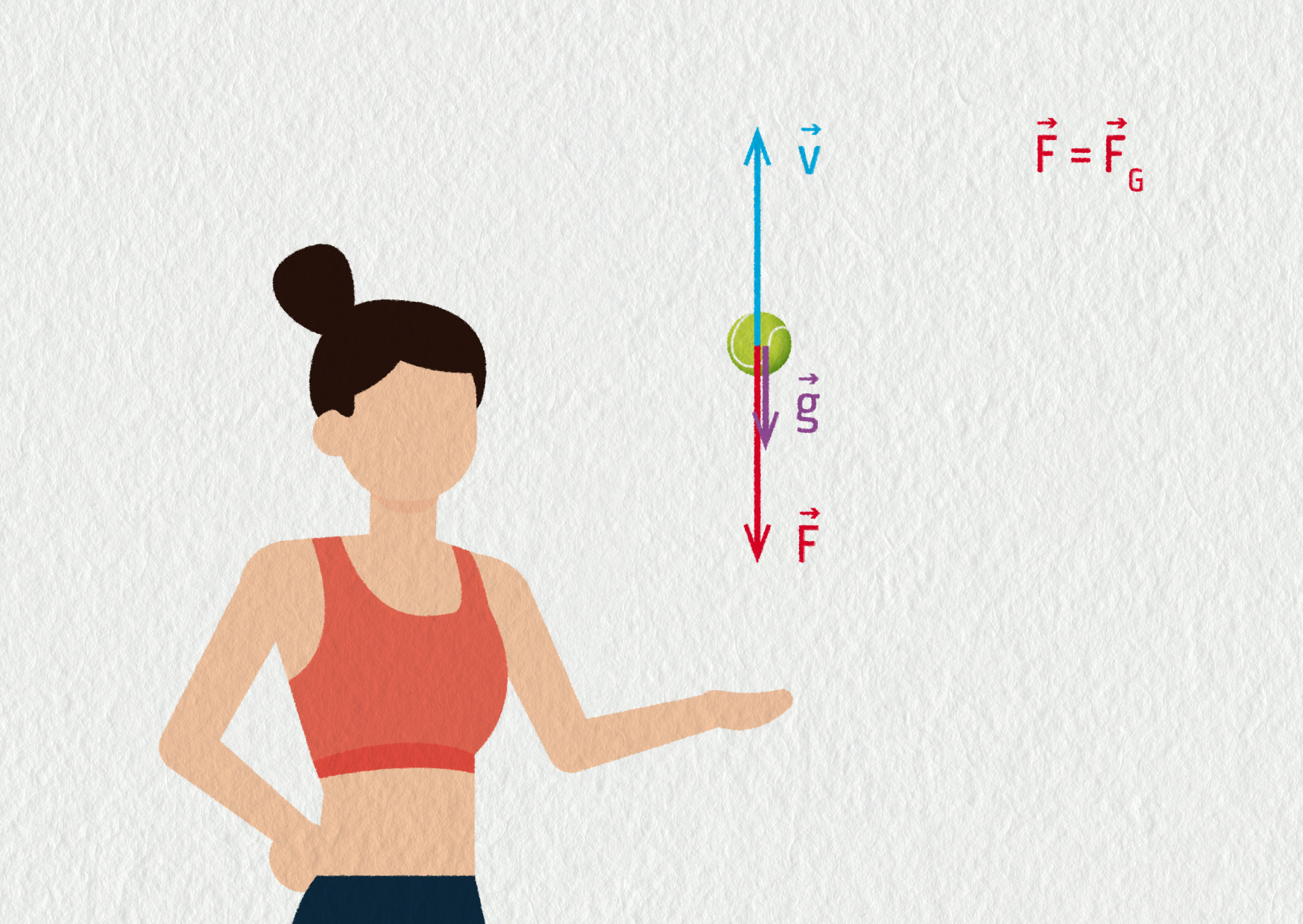
Zdroj
Zdroj
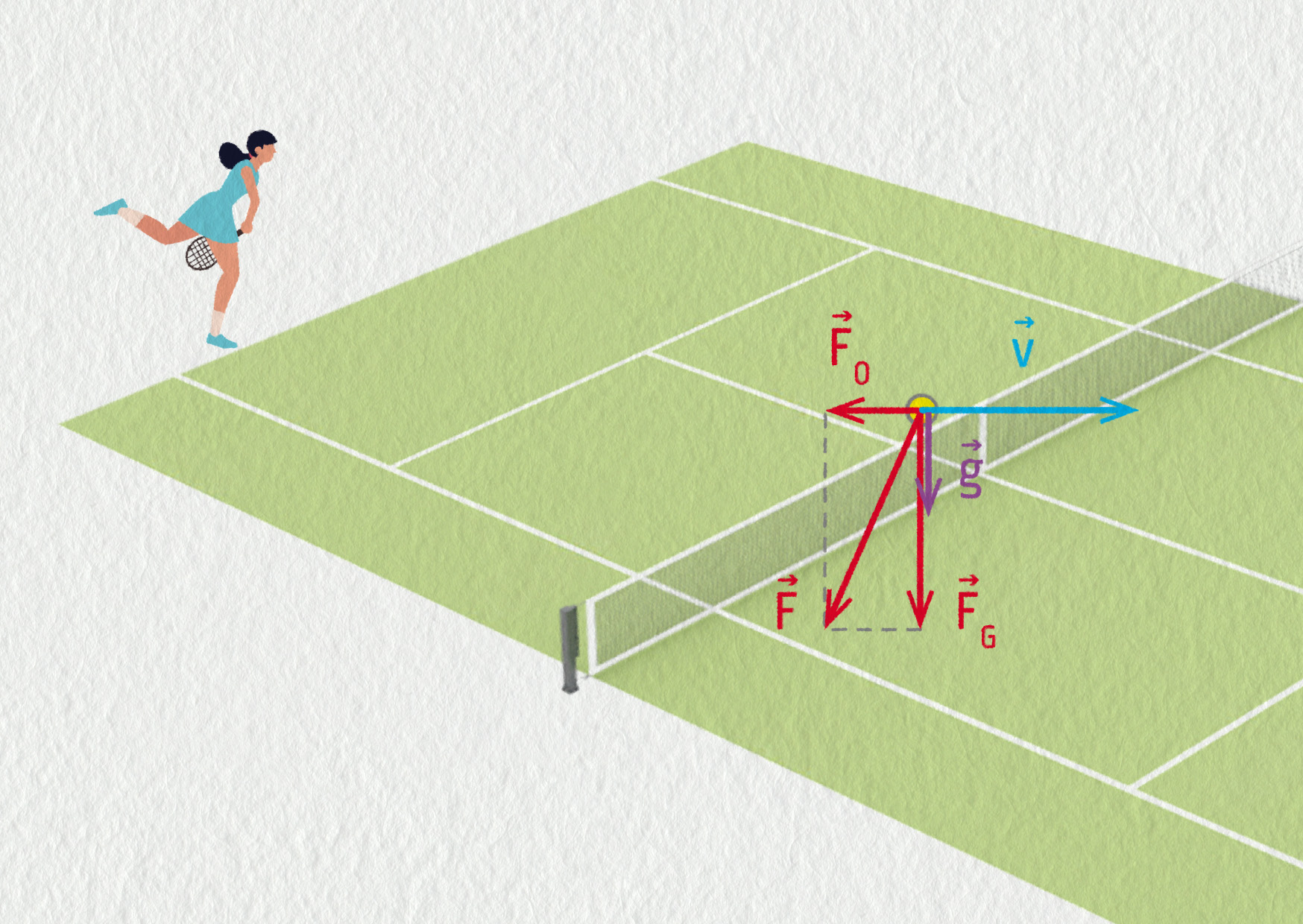
Podobně je tomu i při tenisovém podání. V tomto případě mají vektor rychlosti a vektor výsledné síly zcela jiný směr.
Jaký je význam druhého Newtonova zákona?
Vztah \(F=ma\) spojuje tři důležité mechanické veličiny. Můžeme jednotku síly vyjádřit pomocí jednotek dalších veličin. Vidíme, že \(\mathrm{1\ N = kg\cdot m\cdot s^{-2}}\). Síla 1 N tedy udělí tělesu o hmotnosti 1 kg zrychlení 1 m ⋅ s−2.
Nejde tu ale jen o jednotky. Druhý Newtonův zákon je „srdcem“ celé dynamiky, protože spojuje působení okolí (prostřednictvím sil) a změnu pohybového stavu tělesa (pomocí zrychlení). Umožňuje nám vypočítat (a tedy předpovídat) budoucí pohyb tělesa na základě znalosti jeho počátečního stavu a všech působících sil. Podobně ho můžeme použít i obráceně: známe-li pohybový stav tělesa, dokážeme vypočítat působící síly.
V těch nejjednodušších případech se pohybuje jen jedno těleso a působící síly se nemění. Pak postupujeme zhruba takto:
- Ujasníme si, které těleso budeme sledovat a jakými silami na něj jeho okolí působí. Vezmeme v úvahu dotýkající se pevná tělesa (tlak, tření), okolní tekutinu (odpor vzduchu, tlakové síly) a silová pole (gravitační, elektrické, magnetické).
- Nakreslíme silový diagram pro dané těleso, tj. zaznamenáme všechny působící síly co do velikosti a směru. Určíme výslednou sílu. Těleso zakreslujeme jako bod (nezahrnuje rotaci).
- Aplikujeme správně druhý Newtonův zákon – určíme zrychlení tělesa. Známe-li počáteční rychlost, můžeme odpovědět na otázku, jak se bude těleso pohybovat.
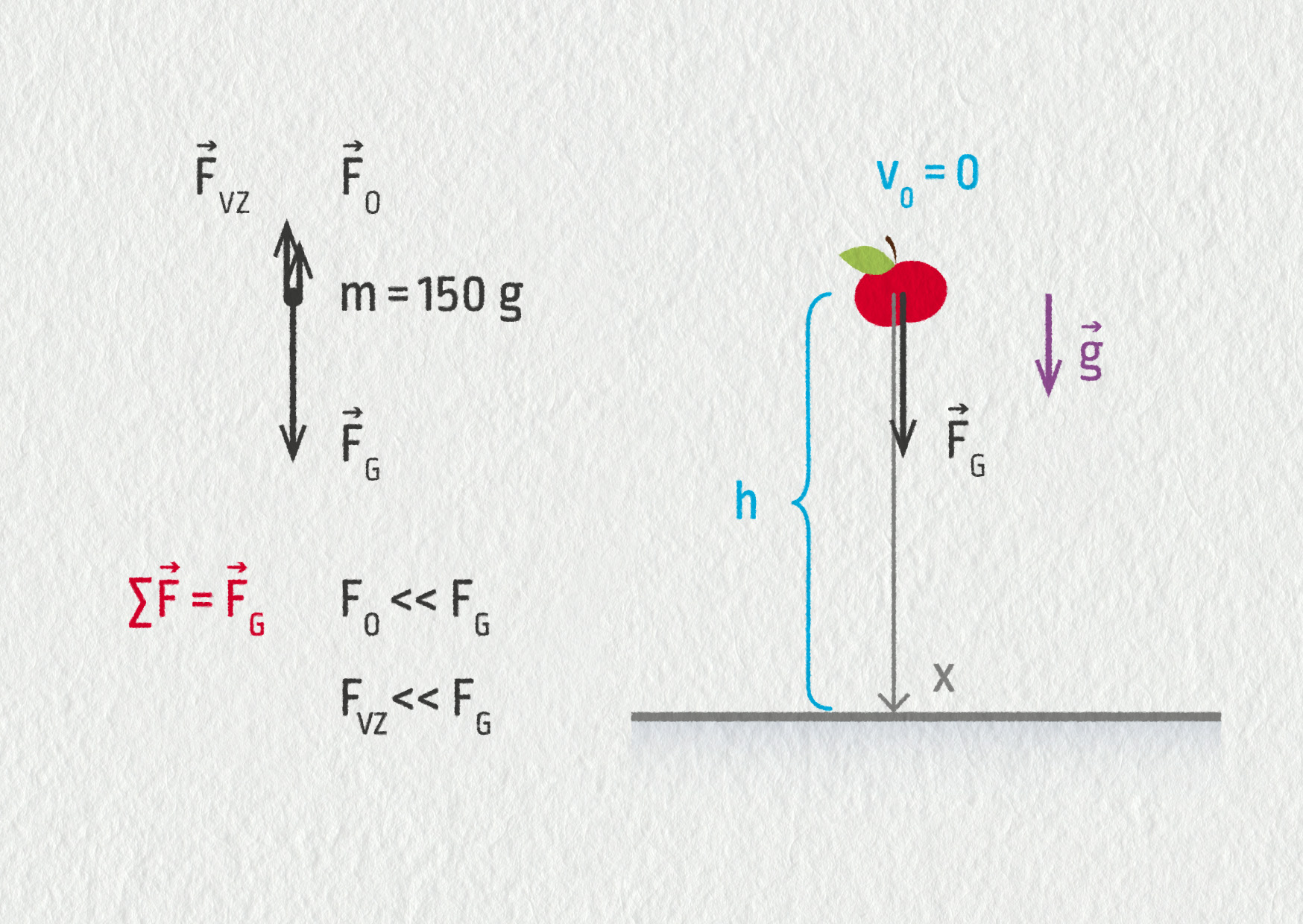
Prozkoumejme společně docela běžnou situaci – jablko padající ze stromu. Určeme na základě pohybových zákonů, za jak dlouho jablko o hmotnosti 150 g dopadne na zem z výšky 3,2 m a jakou bude mít při dopadu rychlost.
1) Studovaným tělesem je jablko. Naše studium začínám ve chvíli, kdy se uvolní od stromu. Nemá tedy žádnou počáteční rychlost, protože až doposud poklidně viselo na větvi. Zkoumáme-li působící síly, můžeme jmenovat tíhovou sílu, která ho přitahuje k zemi, a také vztlakovou sílu, která ho vytlačuje vzhůru. Odhadněme velikosti těchto sil: \(F_\mathrm{G}=1{,}5\ \mathrm{N}\), \(F_\mathrm{VZ}\sim2{,}5\cdot10^{-3}\ \mathrm{N}\). Vidíme tedy, že velikost vztlakové síly můžeme vůči velikosti tíhové síly zanedbat. Neměli bychom zapomenout ani na odporovou sílu vzduchu. Její velikost je však pro velikost jablka a krátkou dráhu pádu přibližně 0,07 N, proto ji opět oproti tíhové síle zanedbáme. Můžeme tedy prohlásit, že na jablko působí pouze tíhová síla – jde o volný pád.
2) Výslednice sil má tedy směr tíhové síly, působí svisle dolů a její velikost je přibližně \(F_\mathrm{G}=1{,}5\ \mathrm{N}\) pro 150 g jablko.
Zdroj
3) Podle druhého Newtonova zákona je výslednice všech sil \(\Vec{F}=m\Vec{a}\). Protože pro tíhovou sílu platí \(\Vec{F}_\mathrm{G}=m\Vec{g}\), porovnáním obou vztahů dostáváme \(\Vec{a}=\Vec{g}\). Druhý Newtonův zákon nám umožnil vyjádřit vlastnosti vektoru zrychlení. Je svislé, směřuje dolů a má velikost a = g = 9,81 m/s2. To znamená, že během každé sekundy svého pádu jablko zrychlí přibližně o 10 m/s. Všechna tělesa, ať mají jakoukoliv hmotnost, budou padat stejně.
Známe-li výšku stromu, můžeme za použití kinematických vztahů pro rovnoměrně zrychlený pohyb předvídat, jak se bude jablko pohybovat v libovolný okamžik, tedy i zodpovědět naše otázky:
\[ \begin{aligned} a&=g\\ v&=gt\\ x&=\frac{1}{2}gt^2 \end{aligned} \]Při dopadu má jablko souřadnici rovnou jeho počáteční výšce nad zemí (x = h = 3,2 m), proto \(h=\frac{1}{2}gt_\mathrm{D}^2\), a proto pro čas dopadu tD lze odvodit
\[t_\mathrm{D}=\sqrt{\frac{2h}{g}}=0{,}81\ \mathrm{s}\;.\]Pro rychlost vD při dopadu pak \(v_\mathrm{D}=gt_\mathrm{D}=7{,}9\ \mathrm{m}\cdot\mathrm{s}^{-1}\).
V tabulce vidíte přehled skutečných hmotnosti a tahu motorů několika dopravních letadel.
- Dopočítejte maximální možné zrychlení všech letadel.
- Proč bude skutečné zrychlení letadel ve skutečnosti o něco menší?
| letadlo (druh motoru) | tah (kN) | hmotnost letadla (t) |
|---|---|---|
| Antonov 124, Ruslan (motor CF6-80C2) | 4 × 276 = 1104 | 405 |
| Boeing 777-Freighter (motor GE90-115B) | 2 × 514 = 1028 | 347 |
| Airbus A380-861 (motor GP7270) | 4 × 310 = 1240 | 575 |
| Boeing 777-300 (motor CFM56-3 series) | 2 × 200 = 400 | 156 |
Použijeme 2. Newtonův zákon. Podle něj můžeme velikost zrychlení letadla vyjádřit pomocí \(a=F/m\).V případě letadla Ruslan má zrychlení hodnotu
\[a=\frac{4\cdot276\,000\ \mathrm{N}}{405\,000\ \mathrm{kg}}=2{,}73\ \mathrm{m}/\mathrm{s}^2\;.\]Pro další letadla pak 2,96 m/s2, 2,16 m/s2 a 2,56 m/s2.
Ve skutečnosti bude zrychlení letadla o něco menší, protože i když bychom chtěli použít maximální možný tah, budou na letadlo působit také odporové síly, a celkové zrychlení bude menší.
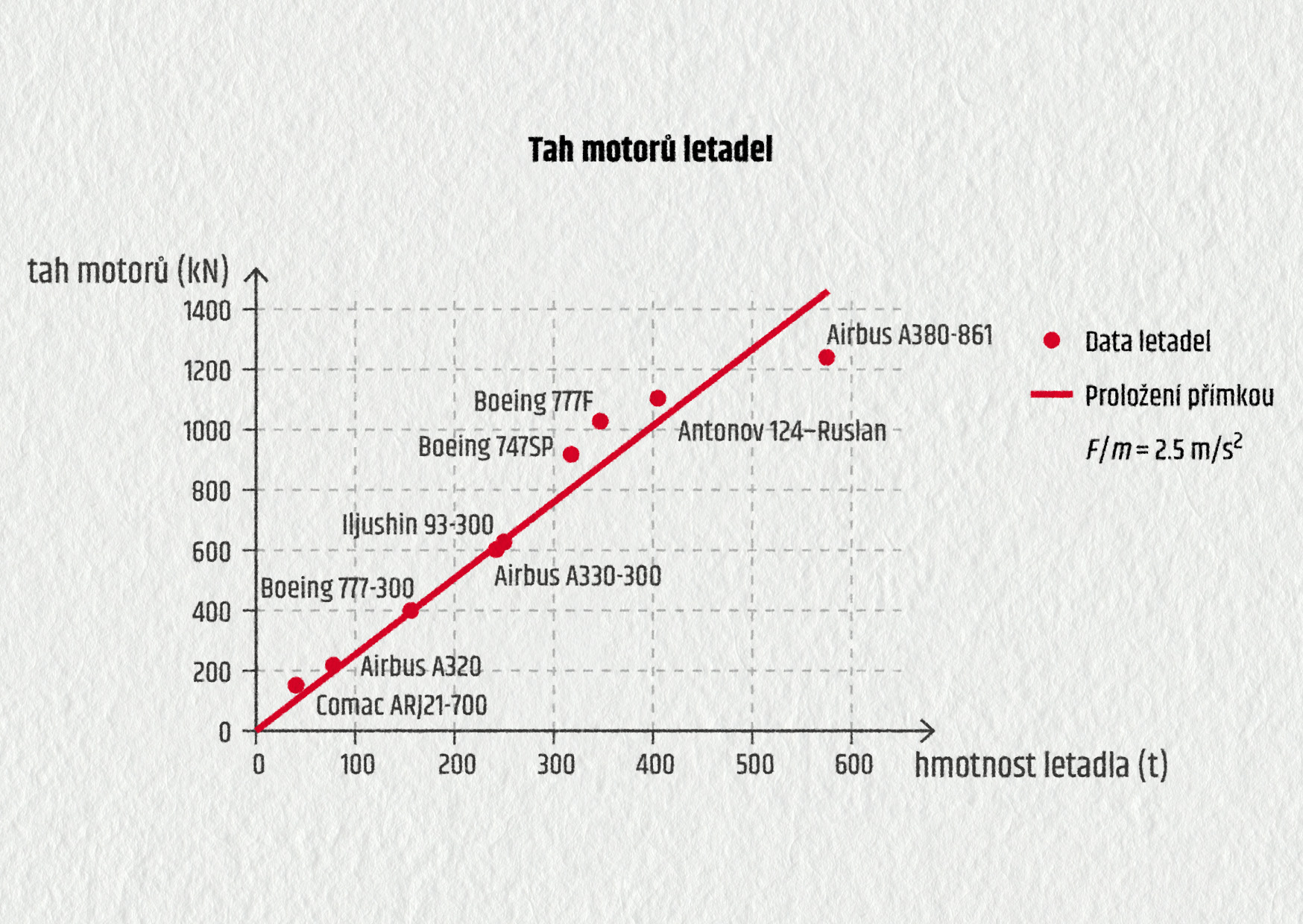
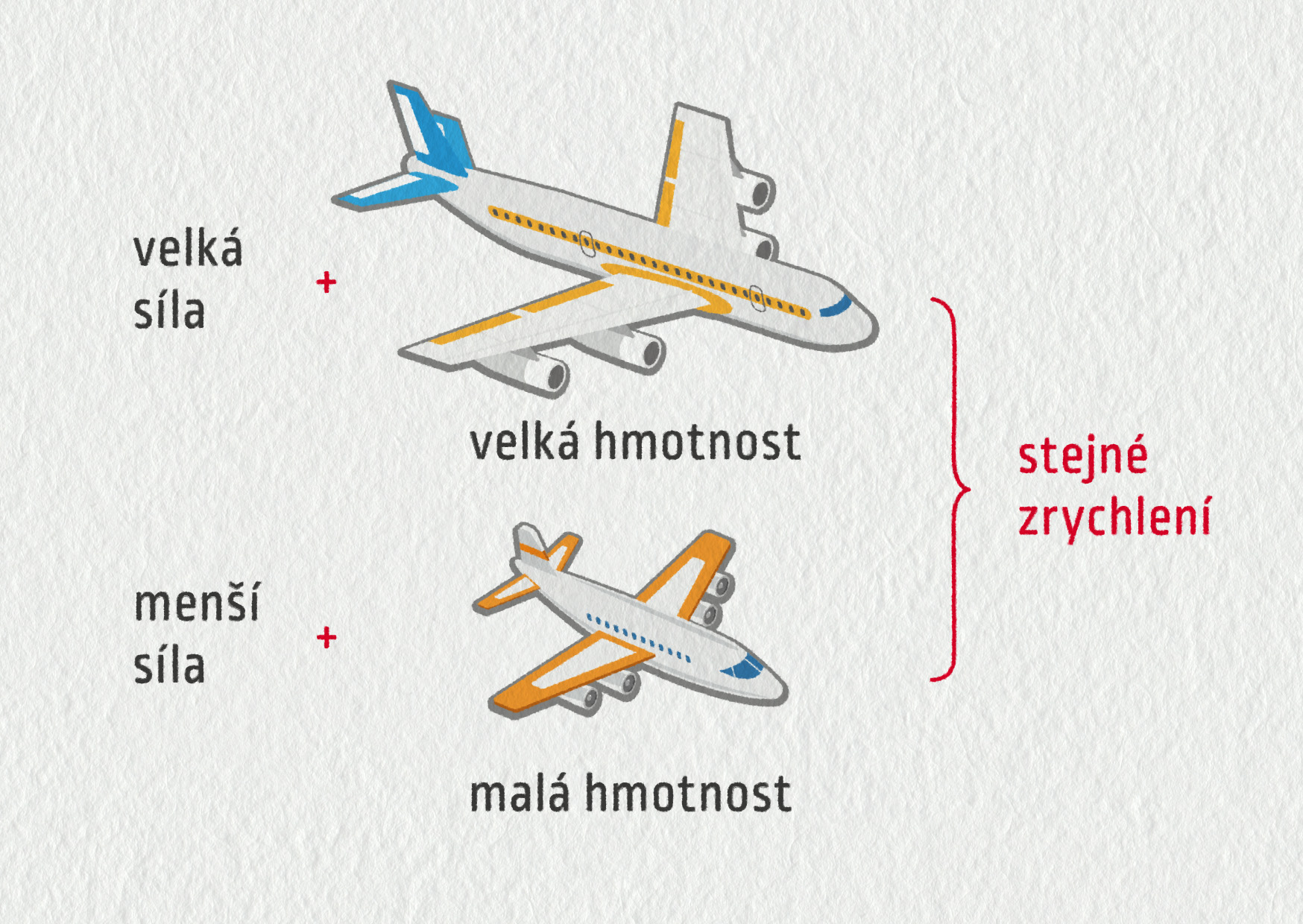
Tah motoru a hmotnost vybraných letadel můžeme znázornit v grafu. Je vidět, že větší hmotnost letadla vyžaduje silnější motor (větší tah). Jejich zrychlení je však přibližně stejné.
Zdroj
Zdroj
Startovací dráha letiště Václava Havla v Ruzyni má délku 3 200 m. Letadlo Airbus A380 o maximální vzletové hmotnosti 569 tun se musí rozjet na rychlost 320 km/h, aby dosáhlo dostatečného vztlaku. Jaký stálý tah by měly mít jeho čtyři motory, když se zvedne od země po ujetí 2 800 m? (Pro jednoduchost odporové síly neuvažujte.)
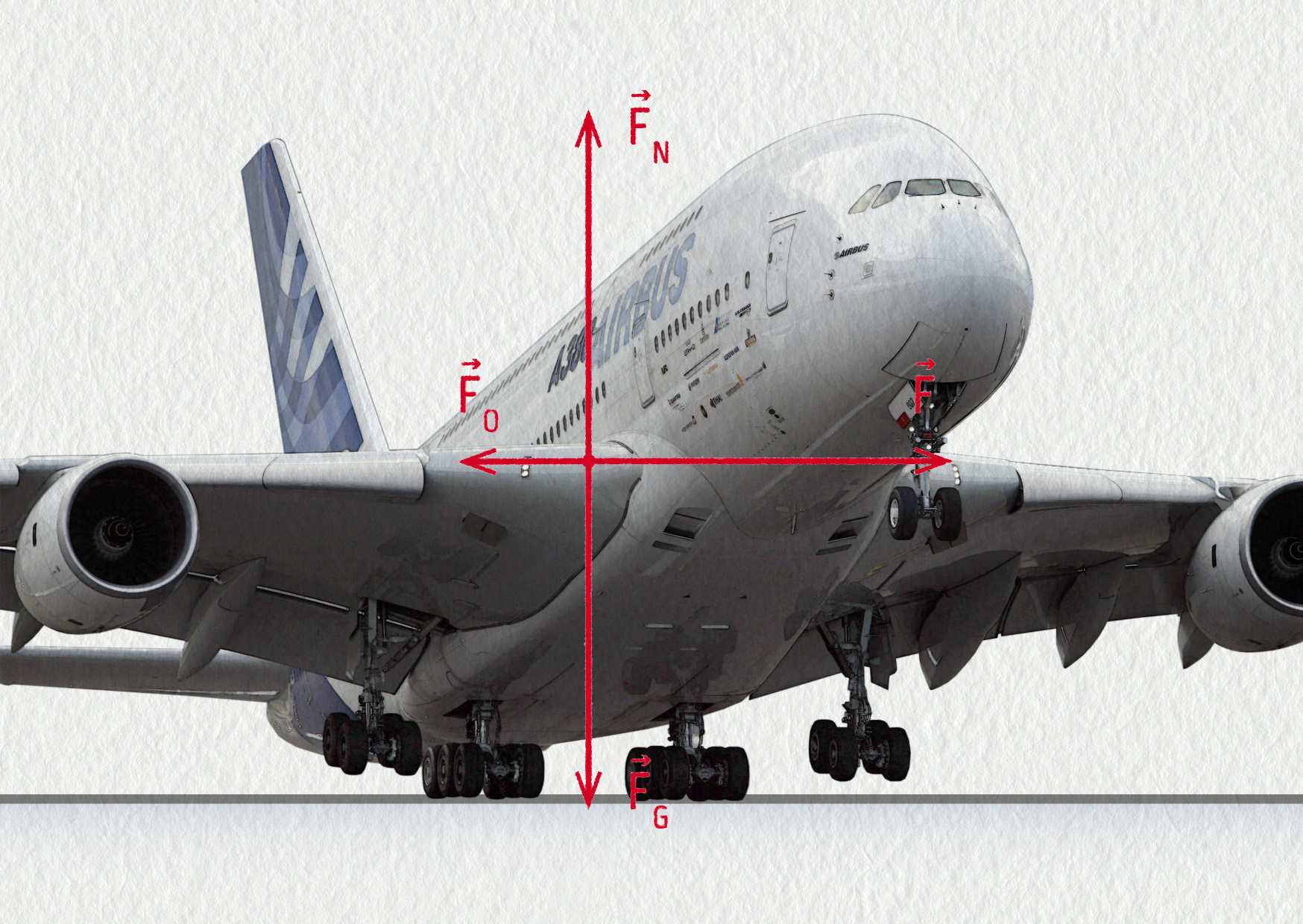
Nejprve se podívejme, jaké síly na startující letadlo působí:
Zdroj
Jde o tíhovou sílu \(\Vec{F}_\mathrm{G}\) a kolmou tlakovou sílu \(\Vec{F}_\mathrm{N}\), které se při rozjezdu letadla navzájem vyruší. Odporovou sílu, i když bude mít velkou hodnotu, pro zjednodušení příkladu neuvažujeme. Výsledná síla má tedy směr a velikost tahové síly motorů \(\Vec{F}\).
Dráha uražená při rozjezdu letadla, který považujeme za rovnoměrně zrychlený, je s = 2 800 m. (Údaj o délce startovací dráhy je nadbytečný.) Tuto dráhu můžeme vyjádřit vztahem \(s=\frac{1}{2}at^2\). Pro rychlost letadla zase platí \(v=at\). Z druhé rovnice vyjádříme dobu, po kterou se letadlo bude rozjíždět \(t=v/a\), a následně z první rovnice velikost zrychlení
\[a=\frac{v^2}{2s}\;.\]Velikost tahové síly motorů je dána vztahem
\[F=ma=m\frac{v^2}{2s}=569\,000\cdot\frac{89^2}{2\cdot2\,800}\ \mathrm{N}=805\ \mathrm{kN}\]Poznámka: Letadlo Airbus A380 má 4 motory, každý o tahu 310 kN. Letadlo má tedy dostatečně silné motory, aby mohlo na letišti startovat. Létají Airbusy A380 do Ruzyně?
Ester Ledecká, dvojnásobná olympijská vítězka z Pchjongčchangu, se chystá ke svému dalšímu sjezdu Světového poháru. Na startu obávané sjezdovky Hahnenkamm v Kitzbühelu je sklon svahu hned po startu 85 % (úhel 40° vzhledem k vodorovné rovině). Za jak dlouho po startu dosáhne Ester rychlosti 45 km/h, nepočítáme-li se třením mezi lyžemi a sněhem ani s odporem vzduchu?

Zdroj
Zakresleme síly, které na Ester působí na nakloněné rovině (viz silový diagram). Neuvažujeme-li odporovou sílu nebo tření, jsou zde pouze tíhová síla \(\Vec{F}_\mathrm{G}\) a kolmá tlaková síla svahu \(\Vec{F}_\mathrm{N}\). Jejich výslednice \(\Vec{F}\) působí ve směru zrychlení, které je rovnoběžné se svahem. V tomto směru také Ester zrychluje.
V nákresu můžeme vidět, že velikost výslednice F odpovídá jedné odvěsně v pravoúhlém trojúhelníku. Druhá odvěsna má velikost FN, zatímco velikost přepony je rovna velikosti tíhové síly FG. V pravoúhlém trojúhelníku nalezneme také úhel α nakloněné roviny (navzájem kolmá ramena). Proto pro velikost výsledné síly získáme \(F=mg\sin\alpha\).
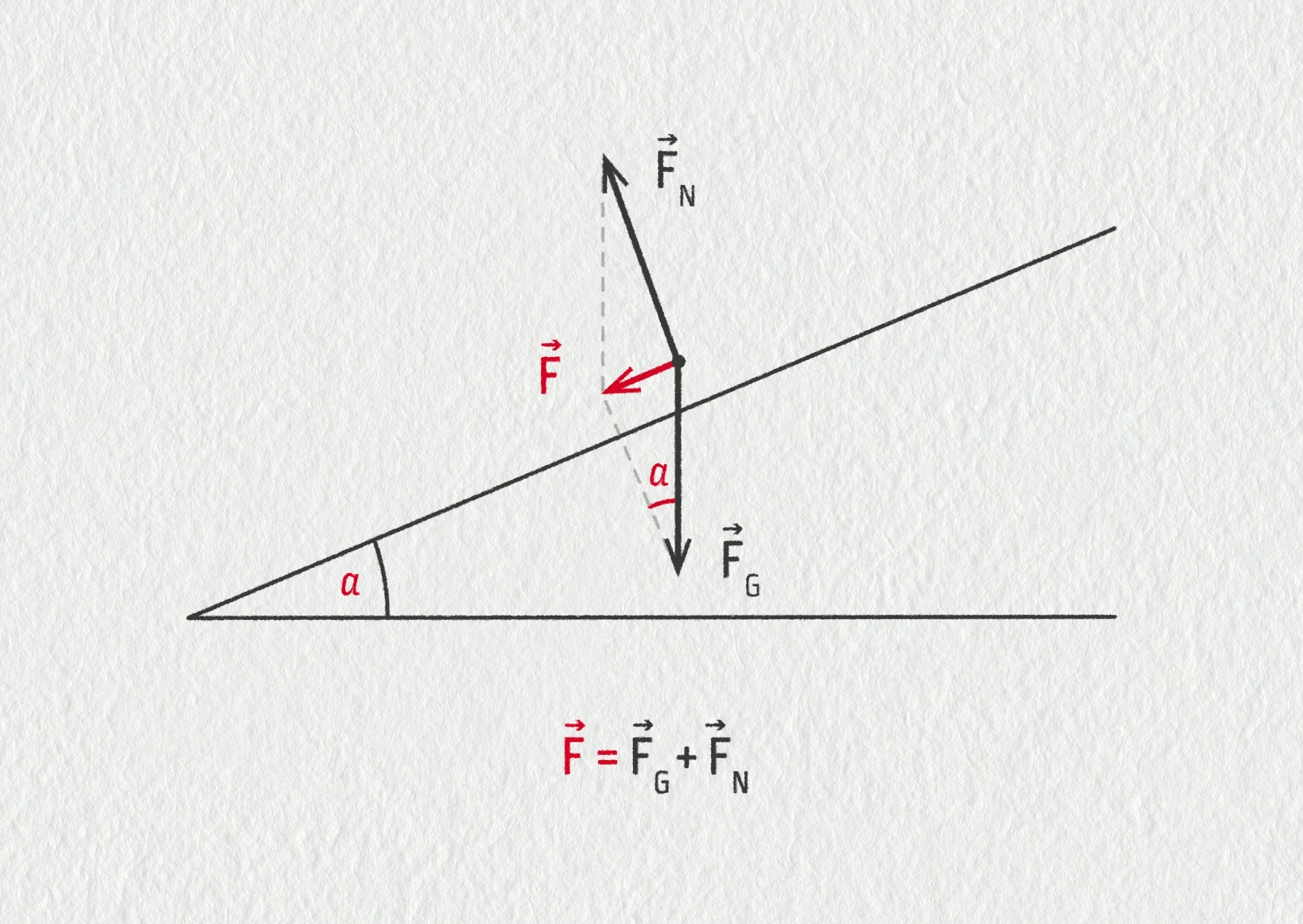
Zdroj
Následně použijeme 2. Newtonův zákon, abychom určili velikost zrychlení Ester: \(ma=mg\sin\alpha\). Můžeme vydělit hmotností m a pro velikost zrychlení tělesa pohybujícího se bez tření na nakloněné rovině získáme vztah \(a=g\sin\alpha\). Většímu sklonu odpovídá větší zrychlení. (Poznámka: pro \(\alpha=90^\circ\) je \(\sin\alpha=1\) a \(a=g\) – těleso přechází do volného pádu.)
Víme tedy, že jde o pohyb rovnoměrně zrychlený (velikost zrychlení je konstantní), rychlost tedy narůstá úměrně času: \(v=at=gt\sin\alpha\). Hledaný čas, ve kterém Ester dosáhne rychlosti 45 km/h = 12,5 m/s, pak vyjádříme
\[t=\frac{v}{g\sin\alpha}=\frac{12{,}5}{9{,}81\cdot\sin40^\circ}\ \mathrm{s}=1{,}98\ \mathrm{s}\;.\]Při střele na bránu se fotbalový míč pohybuje rychlostí 63 km/h. Určete velikost síly, kterou musí brankář působit na míč, aby ho zastavil. Hmotnost míče je 450 g a brankář ho zastaví na dráze 30 cm.
Zdroj
Síla působící na míč v okamžiku zachycení je podle 2. Newtonova zákona úměrná jeho hmotnosti a zrychlení. Velikost zrychlení závisí na tom, jak rychle došlo ke změně rychlosti. Zrychlení je definováno jako \(a=\Delta v/\Delta t\). Změna rychlosti míče má velikost \(\Delta v=17{,}5\ \mathrm{m/s}\), potřebujeme však ještě vyjádřit dobu Δt, po kterou bude brankář působit silou F na míč (předpokládejme, že tato síla je konstantní). Jestliže se míč zastaví na dráze s = 30 cm, pak lze vyjádřit
\[s=\frac{1}{2}a(\Delta t)^2=\frac{1}{2}\frac{\Delta v}{\Delta t}(\Delta t)^2=\frac{1}{2}\cdot\Delta v\cdot\Delta t\;.\]Pro dobu zastavení pak získáme:
\[\Delta t=\frac{2s}{\Delta v}=\frac{2\cdot0{,}30}{17{,}5}\ \mathrm{s}=0{,}034\ \mathrm{s}\;.\]Po dosazení do vztahu
\[F=m\frac{\Delta v}{\Delta t}=0{,}45\cdot\frac{17{,}5}{0{,}034}\ \mathrm{N}=232\ \mathrm{N}\]
