Jak se bude pohybovat těleso, na které nepůsobí žádné síly?
Aristoteles tvrdil, že každý pohyb jednou ustane, protože přirozeným stavem věcí je klid. Aby se těleso pohybovalo, musí na něho působit síla. To se zdá být v pořádku. Pokud při jízdě na kole po rovině přestanete šlapat, po čase se zastavíte. Teprve Galileo Galilei ale správně pochopil podstatu věci. To, že zastavíte, způsobí odpor vzduchu a valivý odpor. Pokud bychom se jich dokázali zbavit, pohyb bude pokračovat pořád dál, do nekonečna. Dobrým příkladem takového tělesa je vesmírná sonda, která letí dopředu setrvačností a zapíná motory, jen pokud potřebuje změnit svoji rychlost. Podobně to platí i pro otáčivý pohyb. Planeta Země se otáčí kolem své osy miliardy let a nepotřebuje k tomu žádný pohon.
Zdroj
Ale vraťme se zpátky na zem. Co se děje s knihou, kterou máte na svém stole? Tíhová síla \(\Vec{F}_\mathrm{G}\) ji nutí padat stále dolů, zatímco kolmá tlaková síla stolu \(\Vec{F}_\mathrm{N}\) se jí v tomto pohybu snaží zabránit. Díky současnému působení obou sil zůstává kniha ležet na stole a nijak se nepohybuje. Říkáme, že silový účinek obou sil se vyrušil. Protože již umíme skládat síly, dokážeme si představit, že součet dvou opačných sil je nulový. Matematicky zapsáno: \(\Vec{F}_\mathrm{G} + \Vec{F}_\mathrm{N} = \Vec{0}\).
Zdroj
Zdroj
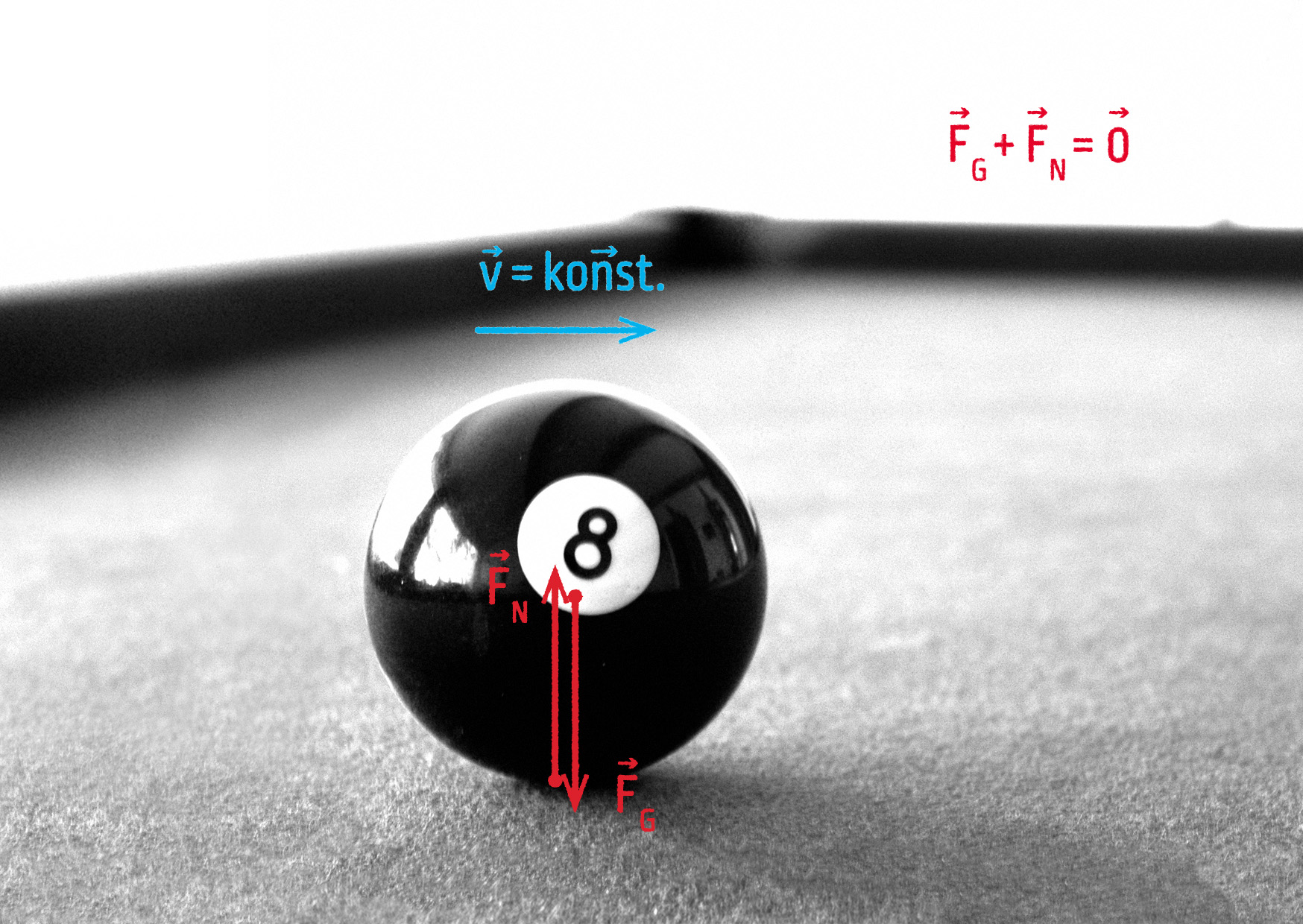
Vezměme nyní kulečníkovou kouli. Uveďme ji do pohybu na vodorovné desce stolu. Koule se pohybuje dopředu, jaké síly na ni působí? Samozřejmě tíhová síla \(\Vec{F}_\mathrm{G}\) působící svisle dolů. Deska stolu ji vyrovnává kolmou tlakovou silou \(\Vec{F}_\mathrm{N}\) svisle vzhůru. Jestliže zanedbáme valivý odpor, koule se pohybuje dopředu, nic ji netáhne, tedy silové působení je stejné jako předtím, kdy se tíhová síla a tlaková síla stolu vyrušily. Bude se pohybovat tak dlouho, dokud nenarazí do mantinelu (další síla), nebo nespadne přes okraj stolu (ztratíme tlakovou sílu stolu). Za těchto změněných podmínek se změní i pohybový stav tělesa.
Tyto situace jsou popsány prvním Newtonovým zákonem – zákonem setrvačnosti:
Každé těleso setrvává v klidu nebo v rovnoměrném přímočarém pohybu, pokud není nuceno vnějšími silami tento svůj stav změnit.
Matematicky můžete tento zákon zapsat ve tvaru \(\Vec{F}=\Vec{0}\,\Leftrightarrow\,\Vec{v}=\mathrm{konst.}\)
Jestliže je výslednice všech sil působících na těleso nulová \(\Vec{F}=\Vec{0}\), pak těleso vykonává rovnoměrný přímočarý pohyb, nebo zůstává v klidu (zvláštní případ rovnoměrného přímočarého pohybu). A stejně to platí i obráceně. Jestliže se těleso pohybuje rovnoměrným přímočarým pohybem, pak se síly, které na něj působí, musí vyrušit. V matematickém vyjádření zákona setrvačnosti je to vyjádřeno znakem ekvivalence ⇔.
Tuto vlastnost všech těles – tendenci zůstávat v klidu či pohybu – nazýváme setrvačnost. Když není důvod ke změně, tak změna nenastane… Dobře ji známe z praxe: městský autobus se rozjede a lidé stojící v něm se naklánějí dozadu, mají tendenci setrvávat na místě, zatímco autobus jim ujíždí pod nohama. Automobil vjíždí do levotočivé zatáčky a pasažéři se mírně vykloní směrem vpravo. Mají tendenci setrvávat v přímočarém pohybu, který vykonávali předtím. A stejně tak i planeta Země, kterou jsme zmínili v úvodu kapitoly, setrvává ve svém otáčivém pohybu.
Poznámka: Z hlediska mechaniky je úplně jedno, jestli na těleso nepůsobí žádné síly nebo jestli se působící síly vyruší. Zákon setrvačnosti platí v obou případech. S tělesem, na které by nepůsobila žádná síla, se však na Zemi nesetkáme, Země bude vždy na těleso působit gravitační silou. Proto budeme vždy uvažovat několik sil, které na těleso působí. Například tíhová síla a tlaková síla stolu pro těleso ležící na stole. Nebo tíhová síla a vztlaková síla vody působící na ledovou kru plující v moři.
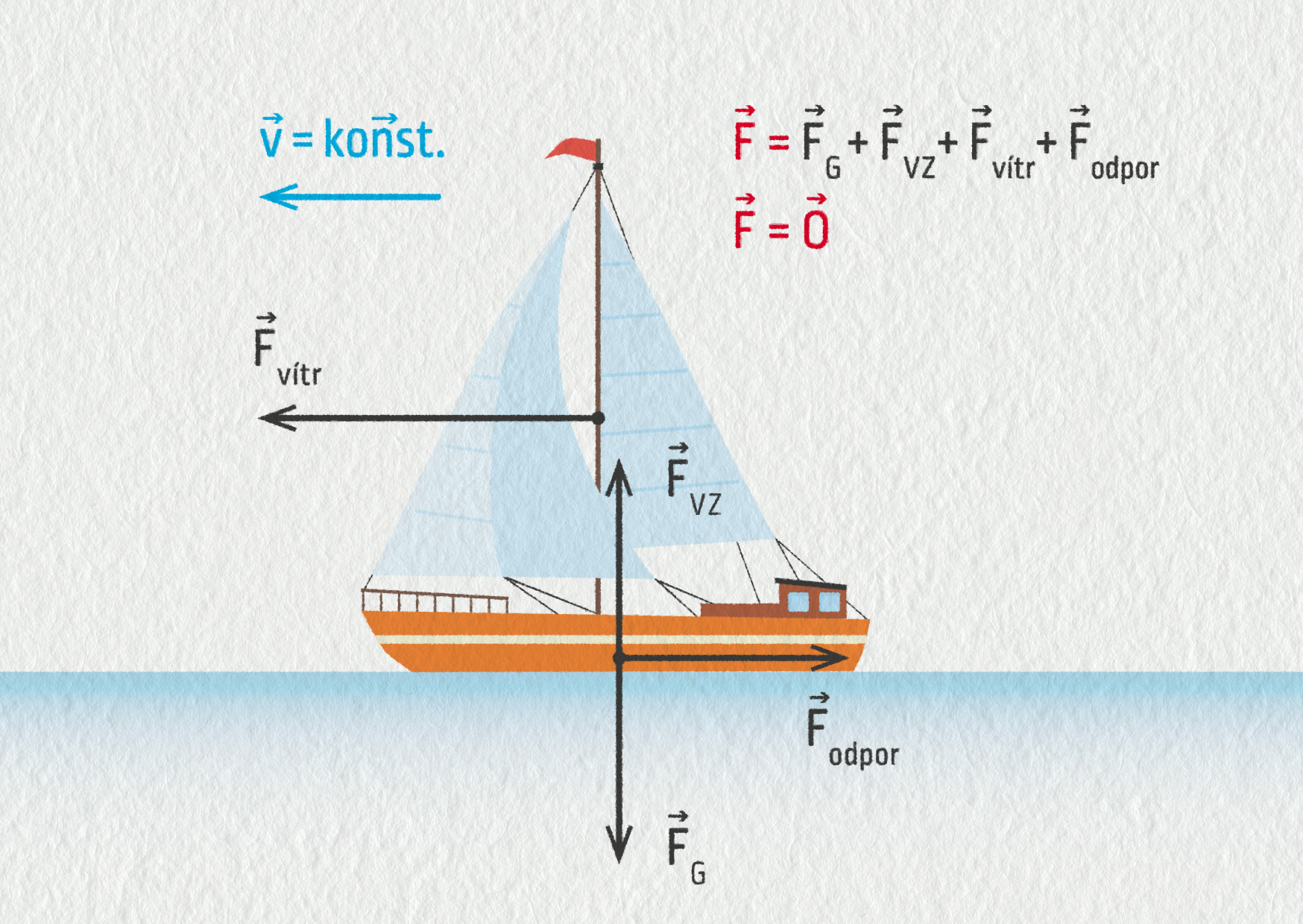
Příklad: Na obrázku 5.16a vidíte plachetnici plující konstantní rychlostí 13 uzlů (přibližně 24 km/h). Její celková hmotnost je 7,8 tun.
Zdroj
Kontrolní otázka
Zdroj
Kontrolní otázka
Zdroj
Kontrolní otázka
Zdroj
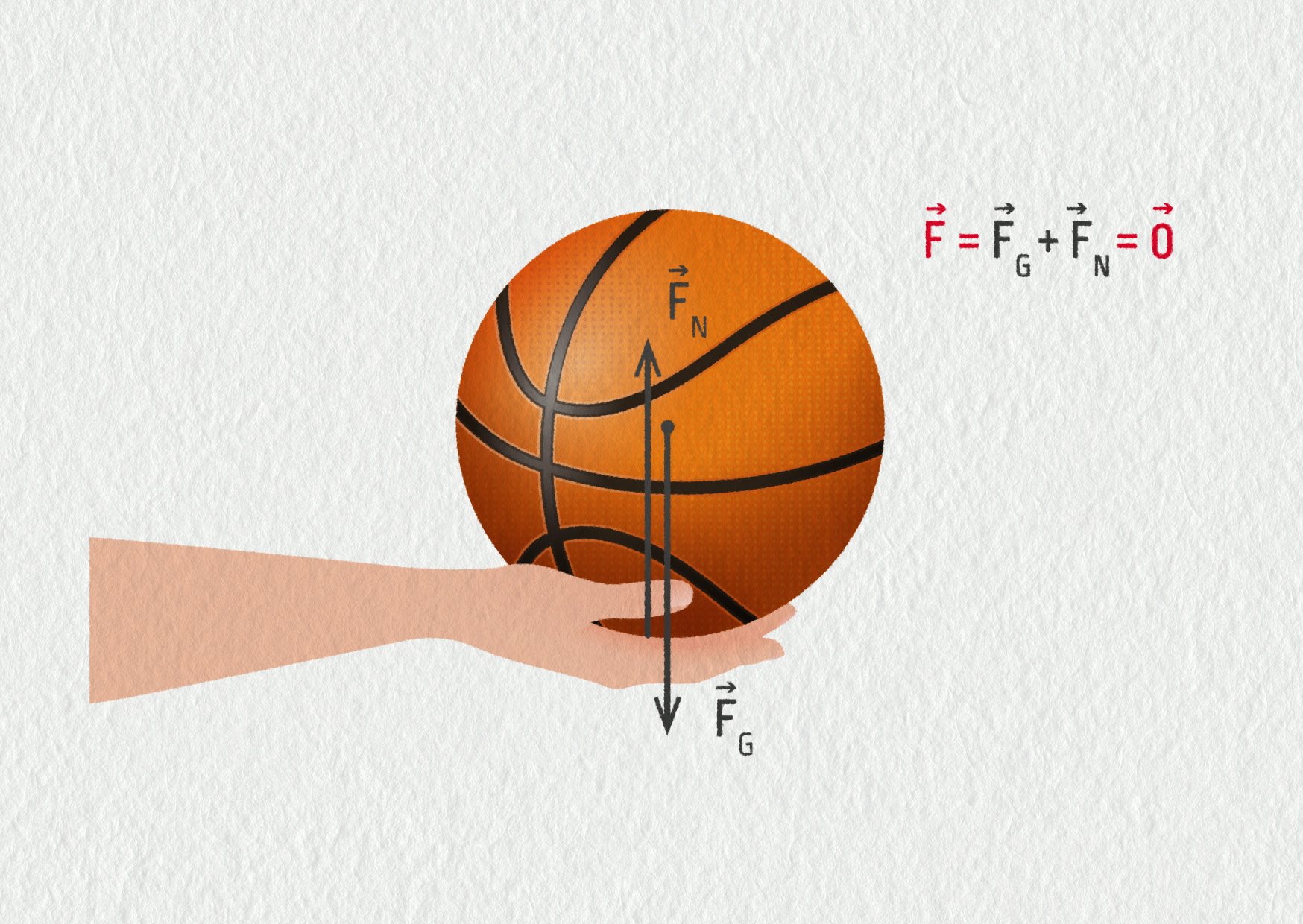
Příklad: Držíte v ruce basketbalový míč o hmotnosti 567 g.
Kontrolní otázka
Zdroj
Kontrolní otázka
Zdroj
Kontrolní otázka
Zdroj
Příklad 1
Příklad: Prozkoumejme ještě malinko složitější situaci. Na svažité ulici vidíme zaparkovaný automobil o hmotnosti 1100 kg. Úhel sklonu vozovky vůči vodorovnému směru α = 15°.
- Zakreslete všechny síly, které na auto působí.
- Určete výslednou sílu.
- Vypočítejte velikosti jednotlivých sil.
Zdroj
Na automobil působí tíhová síla \(\Vec{F}_\mathrm{G}\) (nachází se v gravitačním poli Země), kolmá tlaková síla vozovky \(\Vec{F}_\mathrm{N}\) (díky ní se auto nezabořuje do silnice), a také statická třecí síla \(\Vec{F}_\mathrm{t}\). Třecí síla brání sklouznutí auta po svahu dolů (uvažte, co by se stalo, kdyby byla silnice zledovatělá).
Zaparkované auto setrvává v klidu, takže se podle prvního Newtonova pohybového zákona musí tyto tři síly vyrušit. To znamená, že současné působení \(\Vec{F}_\mathrm{t}\) a \(\Vec{F}_\mathrm{N}\) musí přesně vykompenzovat účinek \(\Vec{F}_\mathrm{G}\). Jinými slovy, sečteme-li vektorově síly \(\Vec{F}_\mathrm{t}\) a \(\Vec{F}_\mathrm{N}\), dostaneme vektor ležící na úhlopříčce rovnoběžníka sil, přesně opačný k vektoru \(\Vec{F}_\mathrm{G}\); viz obrázek – červený vektor. (Poznámka: Pokud by velikost třecí síly mezi pneumatikami automobilu a povrchem silnice překročila maximální hodnotu, auto by začalo klouzat po svahu dolů.)
Pro výpočet velikostí jednotlivých sil jsou důležité pravoúhlé trojúhelníky s přeponou o velikosti \(F_\mathrm{G}\) a odvěsnami o velikostech \(F_\mathrm{N}\) a \(F_\mathrm{t}\). V nich platí
\[\sin\alpha=\frac{F_\mathrm{t}}{F_\mathrm{G}}\quad\hbox{a}\quad\cos\alpha=\frac{F_\mathrm{N}}{F_\mathrm{G}}\]Číselně dostáváme: \(F_\mathrm{G}=10{,}8\ \mathrm{kN}\), \(F_\mathrm{t}=254\ \mathrm{N}\), \(F_\mathrm{N}=10{,}4\ \mathrm{kN}\). Výsledná síla má nulovou velikost. Podle 1. Newtonova zákona se síly musí navzájem vyrušit, protože automobil setrvává v klidu.
