Co platí pro vzájemné působení těles?
V pokusu s vozíkem jsme jej uváděli do pohybu pomocí vnější síly (taháním za provázek). Je ale vůbec možné, aby těleso uvedlo do pohybu samo sebe? Při pohybu lidí, aut či vesmírných raket se s tím běžně setkáváme. Prostě se rozejdete a ani o tom nepřemýšlíte. Pojďme se ale na situaci podívat podrobněji. Z pohledu 2. Newtonova zákona musí na těleso působit jeho okolí tak, aby výsledná síla nebyla nulová. Různé části tělesa na sebe sice mohou působit (stačí se poškrábat na hlavě), ale na pohyb tělesa to nemá vliv. Funguje to tedy takto: člověk se opře do podlahy mírně zešikma, začíná na podlahu působit třecí silou. V tu chvíli začne také podlaha působit na člověka třecí silou opačného směru a ta uvádí tělo do pohybu. Lidé či auta se tedy „odráží“ od podlahy pomocí tření, lodě či letadla od okolní tekutiny pomocí tlakových sil. Využíváme přitom důležitou vlastnost sil, kterou shrnuje zákon akce a reakce:
Dvě tělesa na sebe vždy vzájemně působí stejně velkými, opačně orientovanými silami.
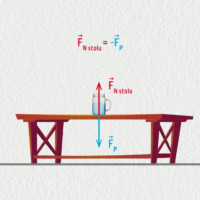
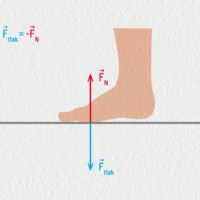
Označíme-li \(\Vec{F}_\mathrm{A}\) sílu, kterou působí těleso A na B a \(\Vec{F}_\mathrm{B}\) sílu, kterou působí B na A, můžeme zákon napsat jednoduše jako \(\Vec{F}_\mathrm{A}=-\Vec{F}_\mathrm{B}\). Pro jejich velikosti pak píšeme \(F_\mathrm{A}=F_\mathrm{B}\). Tyto síly současně vznikají i zanikají, proto nelze rozhodnout, která z nich je „akce“ a která „reakce“.
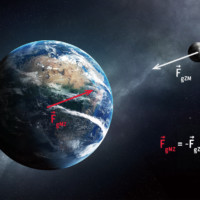
Znázornění akce a reakce
Zdroj
Zdroj
Zdroj
Zdroj
Je důležité připomenout, že síly se trochu nešťastně nazývají akce a reakce, přestože jsou zcela rovnocenné. Jestliže například víme, že Země přitahuje člověka gravitační silou, pak podle třetího Newtonova zákona přitahuje také člověk Zemi stejně velkou silou opačného směru. Tyto síly působí vždy současně, současně vznikají i zanikají. Dobře si prostudujte tyto dva příklady.
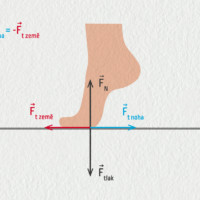
Člověk stojí v klidu na Zemi. Pojmenujte všechny čtyři síly, které se v této situaci objevují. Nakreslete zvlášť silový diagram pro člověka a pro Zemi.
Na člověka působí gravitační síla Země a kolmá tlaková síla Země. Na Zemi pak gravitační síla člověka a tlaková síla chodidel člověka. Viz následující nákres.


Zdroj
Akce a reakce jsou vždy stejné povahy: gravitační na gravitační, třecí na třecí, tlaková na tlakovou. Vzájemně se nevyruší, protože každá tato síla působí na jiné těleso.
Podle 3. Newtonova zákona je působení dvou těles vždy vzájemné. To znamená, že pokud Země přitahuje jablíčko visící na stromě nebo padající dolů, přitahuje stejně velkou silou i jablíčko samotnou Zemi. Z toho plyne, že tak jako padá jablíčko k zemi, měla by i Země padat k jablíčku (dokud se nedotknou)! Dá se něco takového pozorovat?
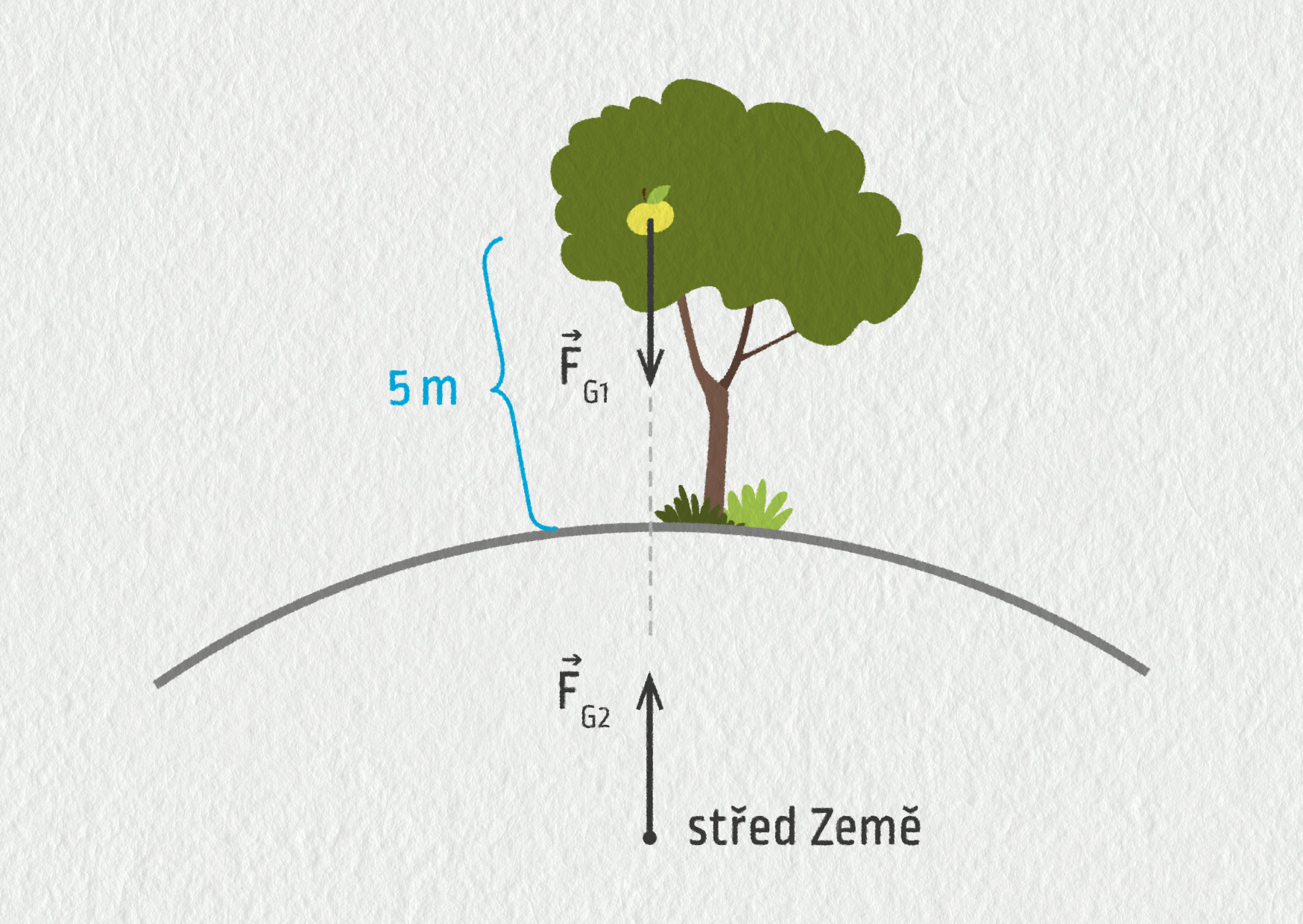
Zdroj
Předpokládejme, že jablíčko (hmotnost m1 = 200 g) padá z výšky 5 m nad povrchem Země (hmotnost m2 = 6,0 ⋅ 1024 kg).
Určete
- za jak dlouho spadne jablko volným pádem,
- s jakým zrychlením padá Země k jablku,
- o kolik se při pádu posune těžiště Země.
a) Jablko je k Zemi přitahováno tíhovou silou \(F_\mathrm{G1}=m_1g=2\ \mathrm{N}\). Po uvolnění padá k zemi rovnoměrně zrychleným pohybem se zrychlením \(a_1=g=10\ \mathrm{m/s^2}\) (zanedbali jsme odpor vzduchu, použijeme zaokrouhlenou hodnotu g). Dráha pohybu \(s_1=\frac{1}{2}gt^2\) je zřejmě rovna výšce, ze které padá. Odtud vypočítáme dobu pádu
\[t=\sqrt{\frac{2s_1}{g}}=1\ \mathrm{s}\;.\]b) Podle 3. Newtonova zákona přitahuje i jablko Zemi silou \(F_\mathrm{G2}=F_\mathrm{G1}=2\ \mathrm{N}\). Jelikož Země není ve vesmíru nijak upevněna, padá k jablku volným pádem se zrychlením
\[a_2=\frac{F_\mathrm{G2}}{m_2}=3{,}3\cdot10^{-25}\ \mathrm{m/s^2}\;.\]3) Za dobu t = 1 s urazí Země rovnoměrně zrychleným pohybem dráhu \(s_2=\frac{1}{2}a_2t^2=1{,}7\cdot10^{-25}\ \mathrm{m}\). Tato dráha je o deset řádů menší než velikost atomového jádra čili naprosto neměřitelná.
Podobně jako jablíčko a Země přitahují se i Země a Slunce. Ve skutečnosti není ani Slunce na pevném místě ve vesmíru, ale obíhají se Zemí kolem společného těžiště. Toto těžiště leží pod povrchem Slunce, uvnitř slunečního pláště. Poznamenejme, že pohyb Slunce ovlivňují i další planety. Jestliže pohybu Země při pádu jablíčka si nevšimneme, v případě hvězdy a kolem ní obíhající planety je tento pohyb již docela dobře pozorovatelný. Astronomové tyto drobné pohyby hvězd využívají k odhalení existence tzv. exoplanet, které kolem nich obíhají.
Člověk stojí na váze, odrazí se, vyskočí a poté dopadne zpět. Váha měří závislost tlakové síly FN (mezi člověkem a váhou) na čase (viz obrázek).
- Určete hmotnost člověka.
- Vysvětlete podrobně tvar grafu ve všech fázích pohybu.
- Vypočítejte, jak vysoko člověk vyskočil.

Zdroj
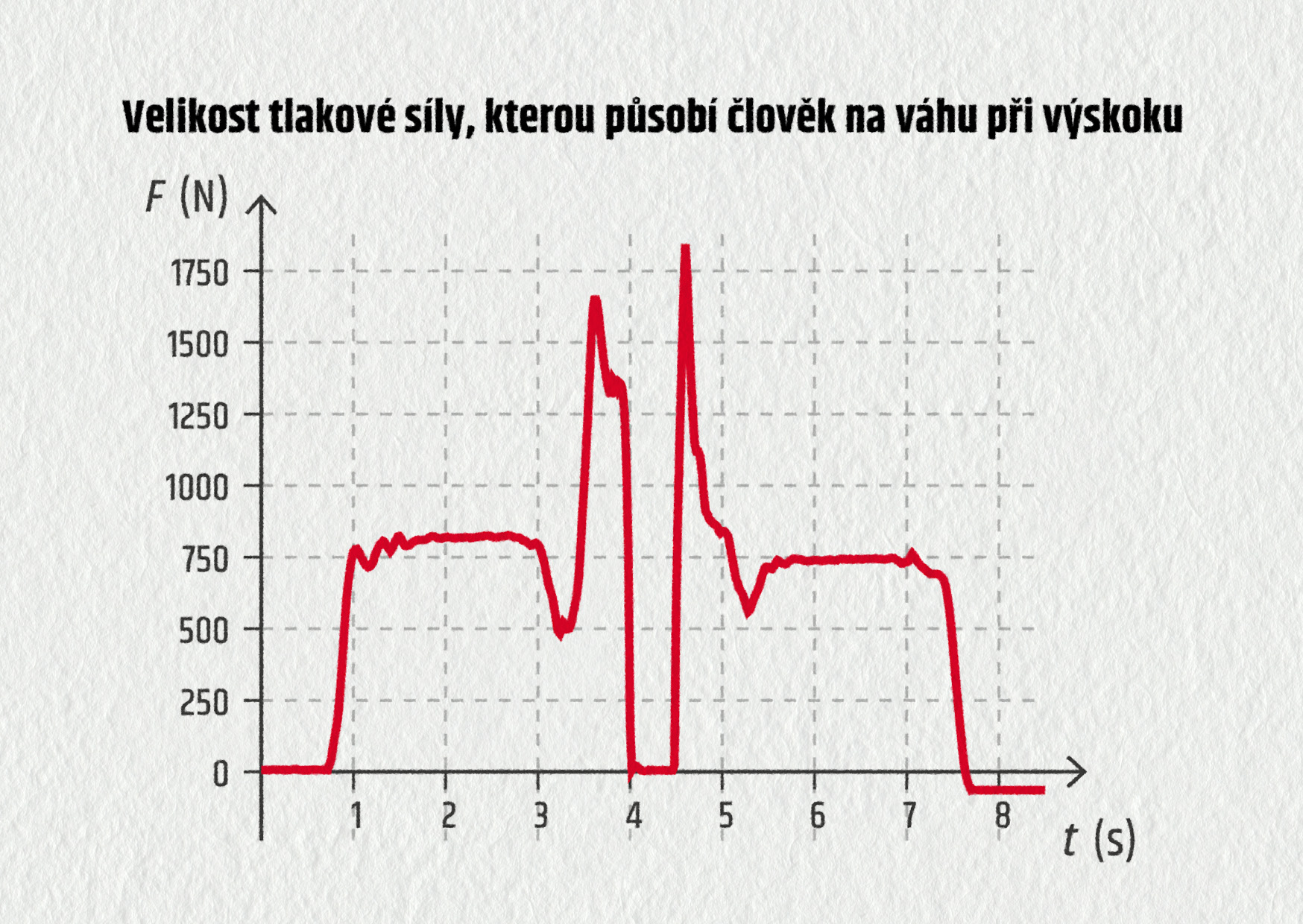
Zdroj
a) Na člověka stojícího na váze působí dvě síly: tíhová \(\Vec{F}_\mathrm{G}\) a kolmá tlaková \(\Vec{F}_\mathrm{N}\). Pokud člověk (jeho těžiště) setrvává v klidu, pak se podle prvního Newtonova zákona tyto síly vyruší, takže \(F_\mathrm{G}=F_\mathrm{N}\). To nastává např. v čase \(t=2\ \mathrm{s}\), z grafu vyčteme \(F_\mathrm{N}=830\ \mathrm{N}\). Pak již můžeme vypočítat jeho hmotnost dle vztahu
\[m=\frac{F_\mathrm{G}}{g}=\frac{830}{9{,}81}\ \mathrm{kg}=84{,}6\ \mathrm{kg}\;.\]b) Z naměřeného grafu můžeme vyčíst následující informace: nejprve člověk stojí v klidu na váze (1). Hodnota síly na váze odpovídá tíhové síle o velikosti 830 N, jak jsme viděli v předchozí otázce. Těsně před skokem se velikost tlakové síly sníží. To je způsobeno tím, že se člověk přikrčí, připravuje se ke skoku, jeho těžiště jde s určitým zrychlením dolů, a proto váha ukazuje menší hodnotu síly, kterou působí na váhu.
Následuje odraz (2), kdy se prudce zvýší tlaková síla. Jde o pohyb zrychlený směrem vzhůru, člověk musí na váhu působit větší silou než je tíhová.

Zdroj
Po odrazu z váhy ukazuje váha nulovou hodnotu (3). Z doby, po kterou byl člověk ve vzduchu, můžeme vypočítat výšku výskoku.
Během dopadu zpět na váhu (4) je síla až dvojnásobná v porovnání s tíhovou, protože tělo člověka se musí zastavit. Člověk na váhu působí mnohem větší silou a podle 3. Newtonova zákona také váha na člověka.
Poslední fází je pak klidové stání na váze (5).
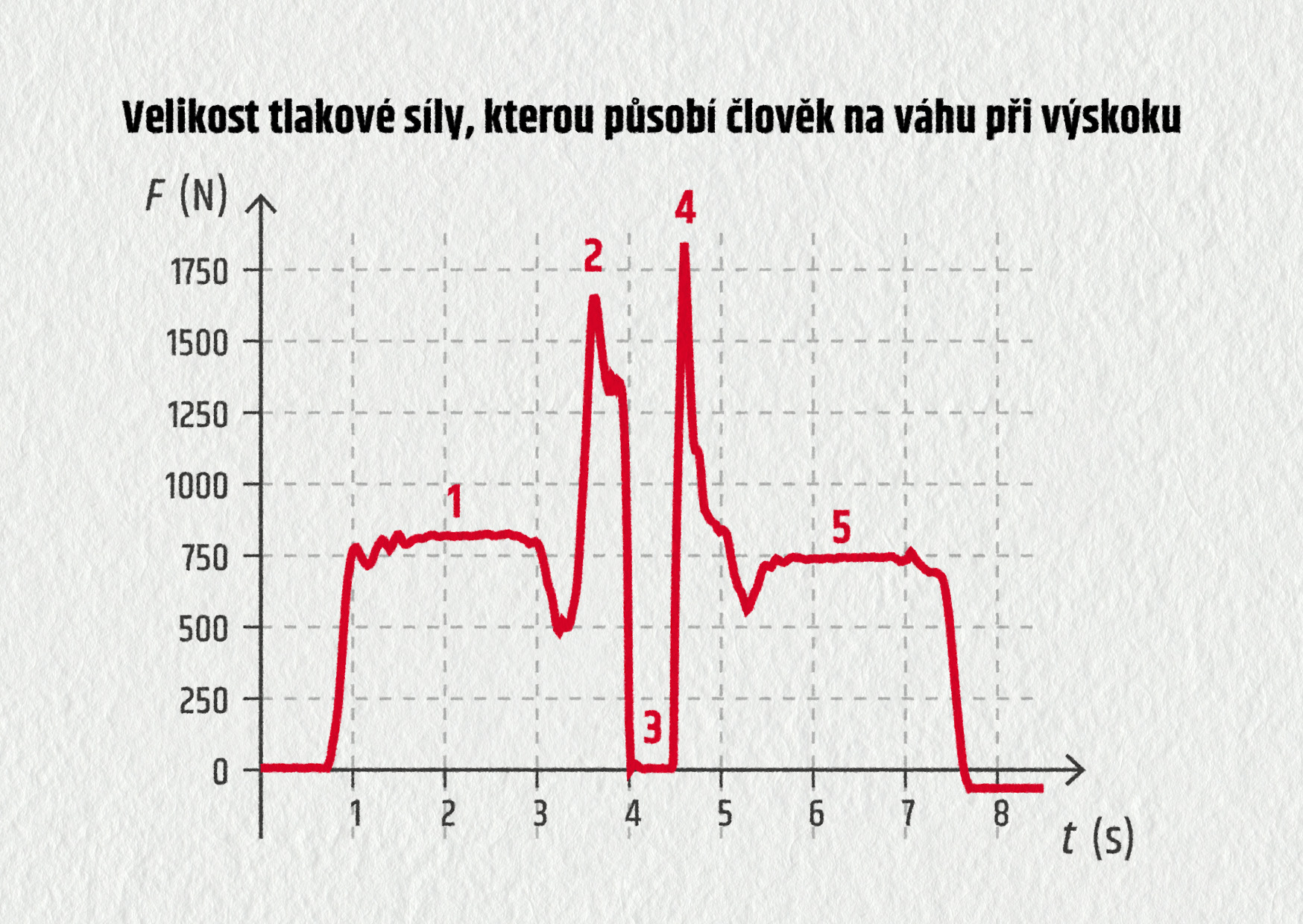
Zdroj
c) Z grafu lze odečíst, že doba výskoku byla \(t=0{,}48\ \mathrm{s}\) (viz detail grafu).
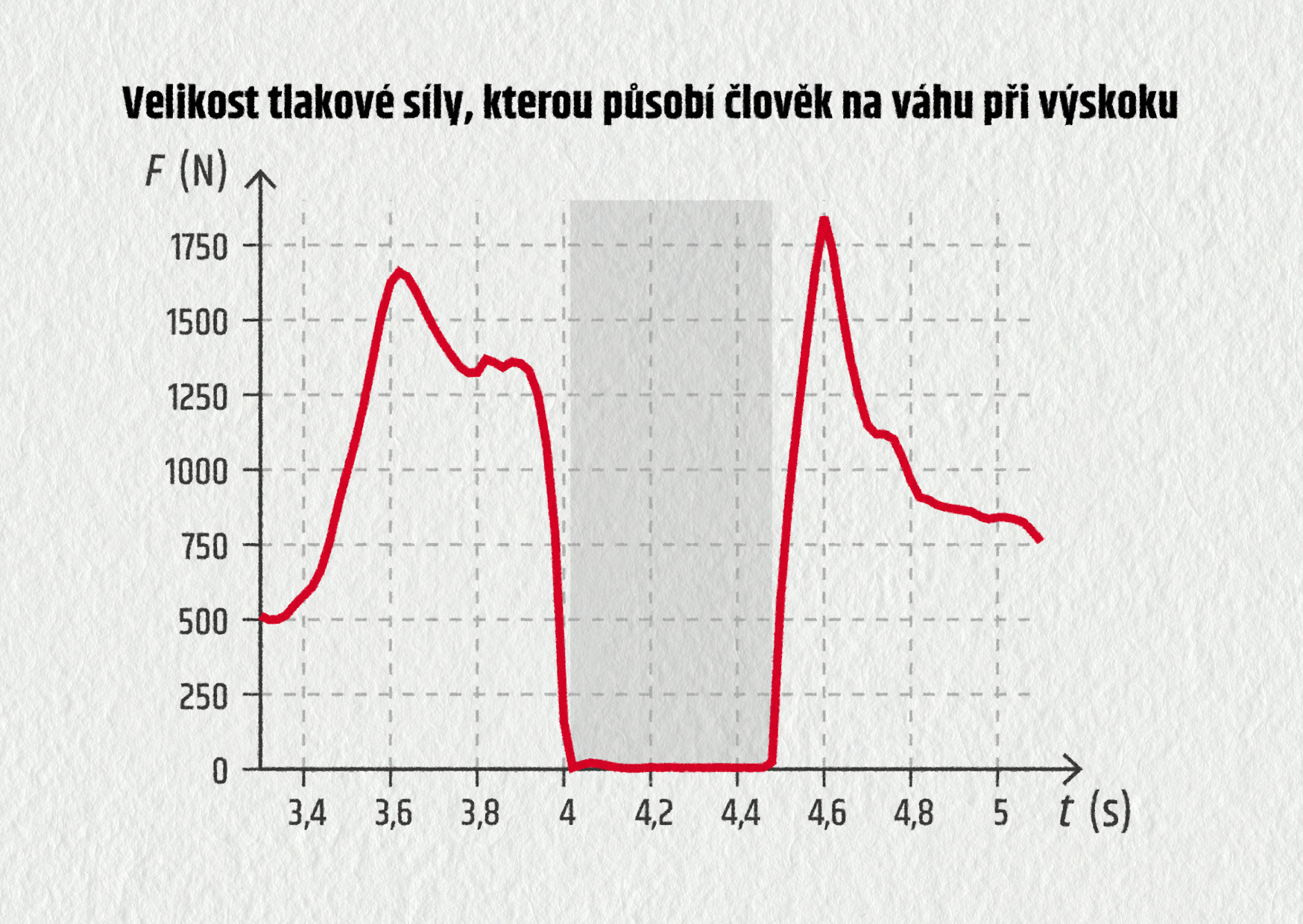
Zdroj
To znamená, že člověk stoupal vzhůru po dobu 0,24 s a padal volným pádem bez počáteční rychlosti opět po dobu 0,24 s. Víme-li, že vzdálenost uražená pohybujícím se tělesem se zrychlením g je vyjádřena vztahem \(s=\frac{1}{2}gt^2\), můžeme snadno spočítat, že výška výskoku byla
\[h=s=\frac{1}{2}\cdot9{,}81\cdot0{,}24^2\ \mathrm{m}=0{,}28\ \mathrm{m}\]Pokud máte k dispozici váhu připojenou k počítači, můžete zkusit uspořádat soutěž o nejvyšší skok. Pro jednoduché porovnání výšky skoků zkuste se žáky „naprogramovat“ výpočet výšky skoku třeba v Excelu.
Co je to tahová síla motoru?
Podívejme se na jedoucí automobil z hlediska silového působení.
Jak víme z obsahu 1. Newtonova zákona, síly se mohou vyrušit i v případě, že těleso je v pohybu. Vezměme například automobil, který jede stálou rychlostí 70 km/h po rovné silnici. Tíhová síla je vyrovnána tlakovou silou silnice a odporové síly (třecí i odpor vzduchu), které působí proti pohybu automobilu, jsou vyrovnány tahovou silou motoru. Automobil se pohybuje rovnoměrným přímočarým pohybem. Namítnete, že automobil nemůže působit sám na sebe silou motoru, a máte pravdu. Pro lepší představu a zjednodušení úlohy jsme sáhli k tomuto znázornění. Ve skutečnosti motor automobilu přes převodové ústrojí působí silou na pneumatiky, které se snaží otáčet. Jsou z tvrdé gumy, na dobré vozovce neproklouznou, takže při svém otáčení působí na vozovku určitou statickou třecí silou a podle 3. Newtonova zákona pak vozovka musí působit stejně velkou silou na pneumatiky, a tím také na automobil. Tato třecí síla vozovky je hybnou silou automobilu a umožňuje mu, aby se pohyboval. Bez ní by se kola protočila a automobil by se ani nerozjel. S tím jsme se občas potkali při náledí.
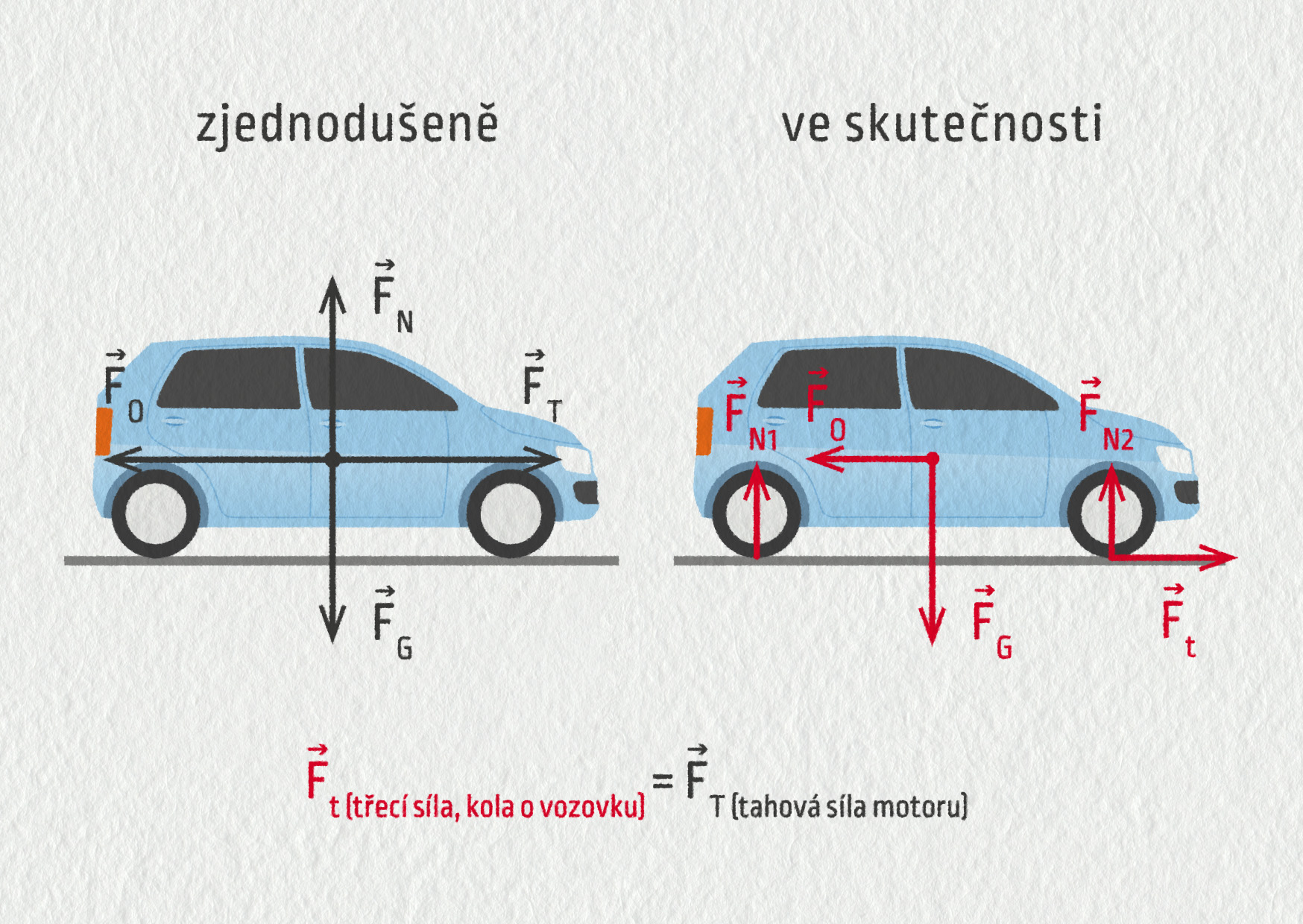
Zdroj

