Po teoretické stránce máme vše, co potřebujeme. Vztahy pro jednotlivé druhy sil a tři pohybové zákony. Prozatím jsme se ale omezili na úlohy, které nevyžadují práci s vektory. Pohybu v rovině a v prostoru se věnujeme samostatně v kapitole 14. Na závěr této kapitoly se ještě podíváme na rozbor situací, kde vystupuje více těles.
Určete zrychlení nákladního vlaku sestávajícího z lokomotivy (např. Škoda ES 499.1 mající hmotnost 87 t, maximální tažnou sílu 176,5 kN) a dvou vagonů (čtyřnápravový vysokostěnný vůz s nákladem o hmotnosti 64 t). Vypočítejte velikosti tahových sil mezi vagony.
Tažná síla lokomotivy je vlastně výslednou silou působící na soupravu o celkové hmotnosti \(M=m_0+2m_1\) \(=87\ \mathrm{t}+2\cdot64\ \mathrm{t}\) \(=215\ \mathrm{t}\). Podle druhého Newtonova zákona tedy dostáváme \(a=F/M=0{,}82\ \mathrm{m/s}^2\).
Síly působící na soupravu rozkreslíme v následujícím schématu:
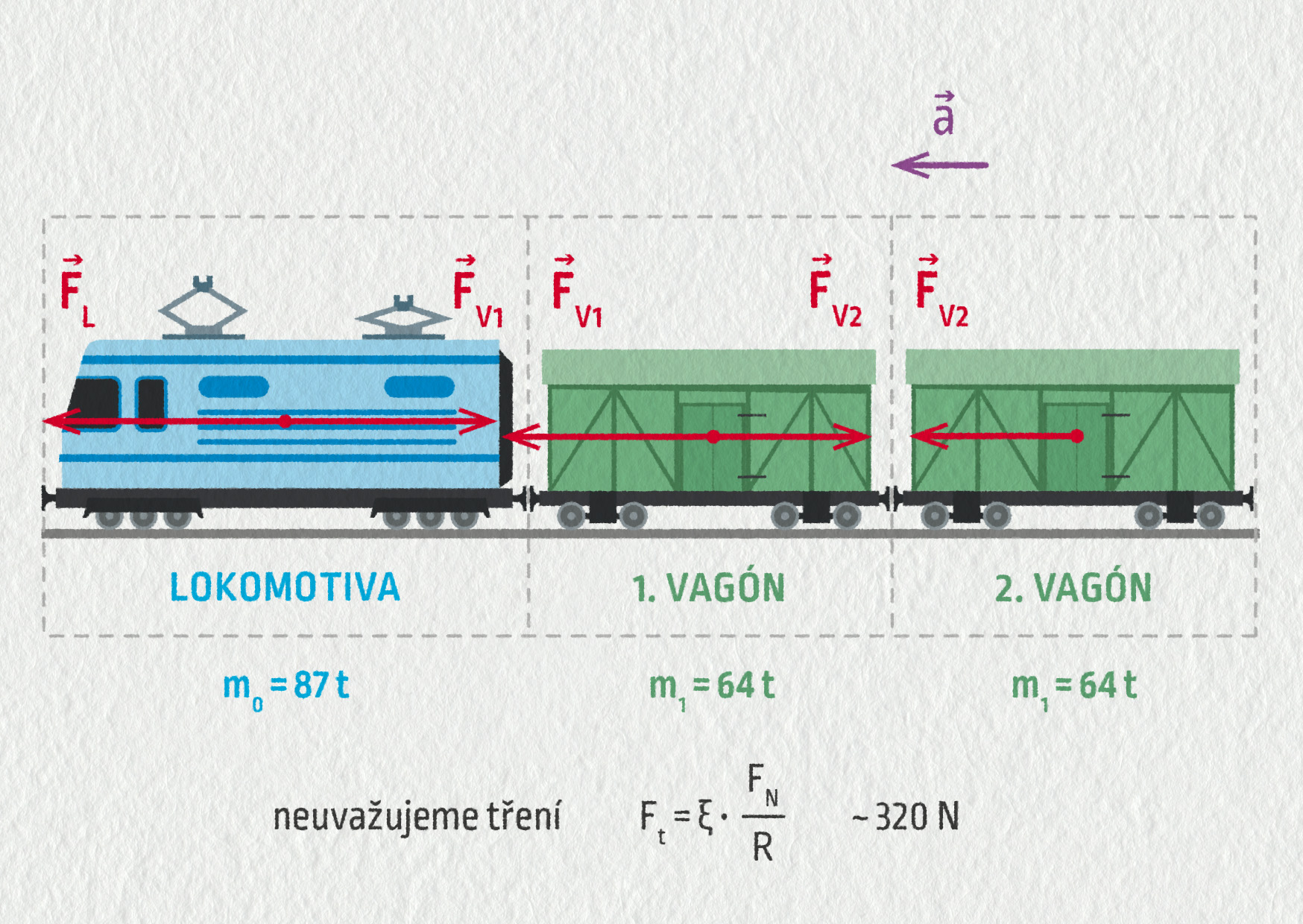
Zdroj
Pro síly mezi vagony pak stačí použít druhý Newtonův zákon a dostáváme:
\[ \begin{aligned} F_\mathrm{V2}&=m_1a=52{,}3\ \mathrm{kN}\\ F_\mathrm{V1}-F_\mathrm{V2}&=m_1a\\ F_\mathrm{V1}&=m_1a+F_\mathrm{V2}=2m_1a=104{,}6\ \mathrm{kN} \end{aligned} \]Dvě závaží o hmotnostech \(m_1=2{,}0\ \mathrm{kg}\) a \(m_2=3{,}0\ \mathrm{kg}\) jsou spojena lanem přes kladku zanedbatelné hmotnosti. Kladka se může otáčet bez tření (viz obrázek). Poté, co soustavu uvolníme, dají se závaží do pohybu. Určete velikost jejich zrychlení a sílu, kterou je lano napínáno.

Zdroj
Zrychlení obou závaží musí být stejné, protože délka lana je stále stejná, obě závaží se pohybují shodně. Těžší dolů, lehčí nahoru. Tahová síla, kterou působí lano na závaží FT, musí být pro obě závaží stejně velká, protože kladka pouze mění směr síly, nikoliv její velikost.
Do obrázku zakreslíme síly, které působí na obě tělesa, stejně jako jejich výslednice \(\Vec{F}_1=\Vec{F}_\mathrm{T}+\Vec{F}_\mathrm{G1}\) a \(\Vec{F}_2=\Vec{F}_\mathrm{T}+\Vec{F}_\mathrm{G2}\).
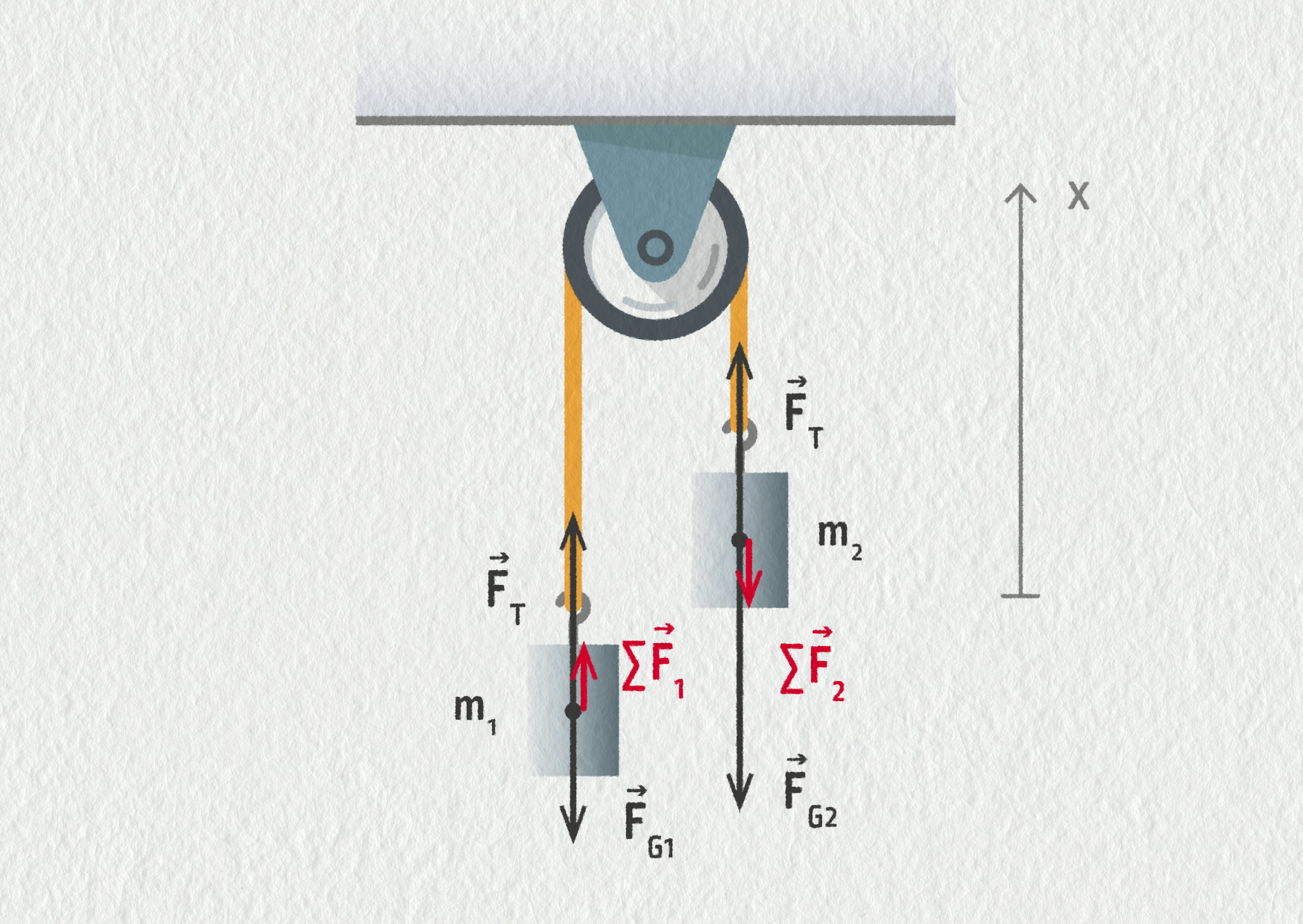
Zdroj
Závaží číslo 1 se bude pohybovat vzhůru (v kladném směru osy x) a závaží číslo 2 se bude pohybovat dolů (v záporném směru osy x). Abychom určili síly působící na lano \(F_\mathrm{T}\) a zrychlení závaží \(a\), použijeme 2. Newtonův zákon a zapíšeme ho zvlášť pro první i druhé závaží:
\[ \begin{aligned} m_1a&=F_\mathrm{T}-m_1g\\ -m_2a&=F_\mathrm{T}-m_2g \end{aligned} \]Tuto soustavu dvou rovnic o neznámých \(F_\mathrm{T}\) a \(a\) můžeme řešit například sčítací metodou. Po odečtení rovnice dostáváme:
\[ \begin{aligned} m_1a-(-m_2a)&=F_\mathrm{T}-m_1g-(F_\mathrm{T}-m_2g)=m_2g-m_1g\\ (m_1+m_2)a&=(m_2-m_1)g \end{aligned} \]Pro velikost zrychlení tedy platí:
\[a=\frac{m_2-m_1}{m_1+m_2}\cdot g=\frac{3\ \mathrm{kg}-2\ \mathrm{kg}}{2\ \mathrm{kg}+3\ \mathrm{kg}}\cdot10\ \mathrm{m/s}^2=2{,}0\ \mathrm{m/s}^2\]Velikost tahové síly lana pak vyjádříme z první rovnice:
\[F_\mathrm{T}=m_1a+m_1g=m_1(a+g)=2{,}0\ \mathrm{kg}\cdot(2{,}0\ \mathrm{m/s}^2 + 10\ \mathrm{m/s}^2)=24\ \mathrm{N}\]Odvoďte, jak se bude pohybovat volně puštěné těleso v gravitačním poli blízko zemskému povrchu (např. kámen padající z věže). Řekněme, že se na začátku pohybu kámen o hmotnosti 270 g nachází ve výšce 17 m nad zemí. Uvolníme ho bez počáteční rychlosti \((v_0=0\ \mathrm{m/s})\) a bude padat v tíhovém poli Země (\(g=9{,}8\ \mathrm{m/s^2}\)). Úlohu řešte
- bez započítání odporu vzduchu (volný pád),
- se započítáním odporu vzduchu (reálný pád).
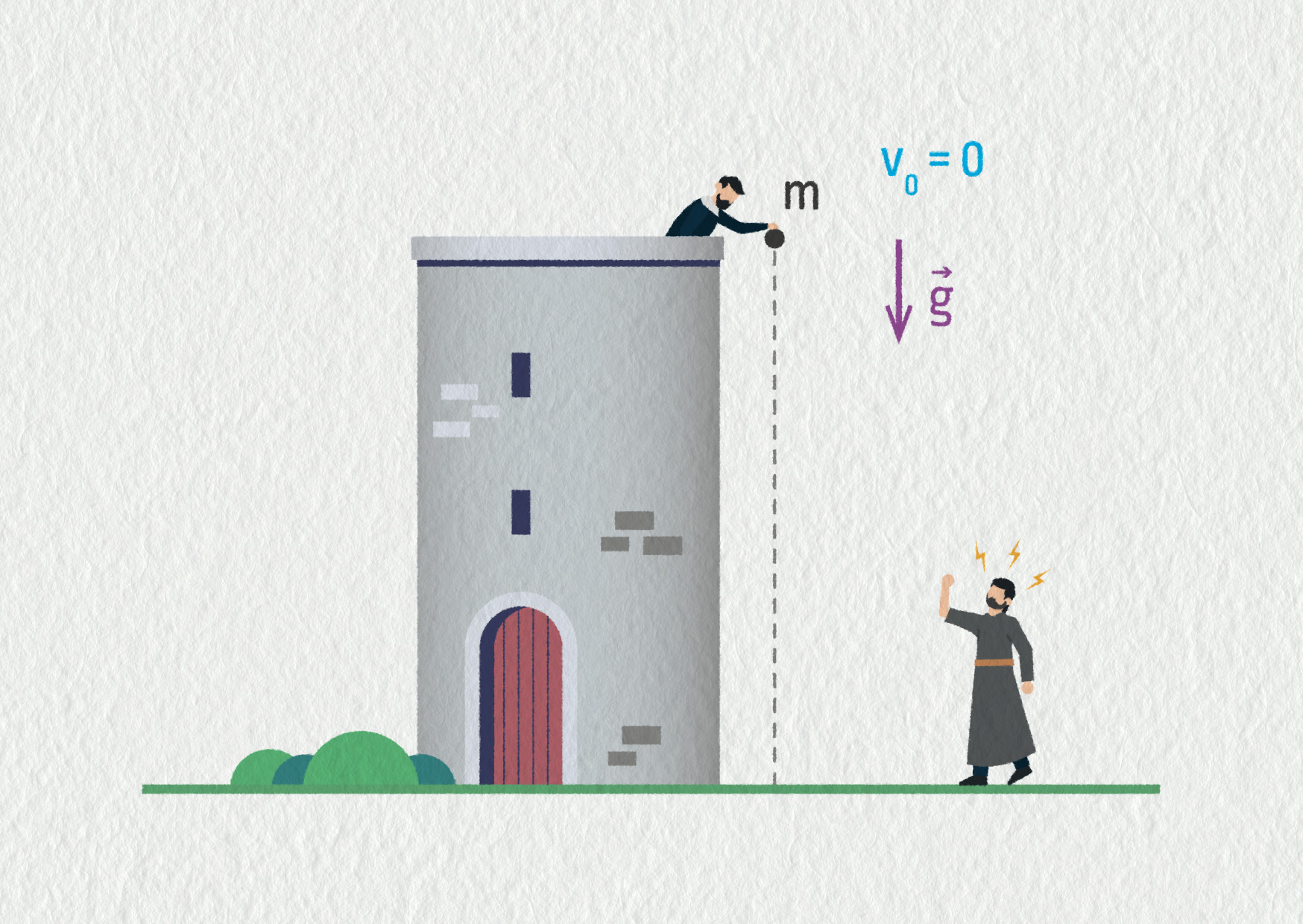
Zdroj
a) Neuvažujeme-li odpor vzduchu, jedinou silou, která uděluje kameni zrychlení (o velikosti g) je tíhová síla o velikosti \(F_\mathrm{G}\). Podle druhého Newtonova zákona je \(F=ma\) a zároveň \(F_\mathrm{G}=mg\). Vidíme, že \(ma=mg\), a po vykrácení rovnice hmotností m dostáváme \(a=g\). Těleso bude tedy padat se stálým zrychlením o velikosti \(a=9{,}8\ \mathrm{m/s}^2\), jeho pohyb bude rovnoměrně zrychlený. Velikost rychlosti bude narůstat přímo úměrně času (viz graf rychlosti na čase).

Zdroj
b) Chceme-li řešit tuto úlohu se započítáním odporu vzduchu, musíme vzít v úvahu další sílu působící na kámen – odporovou sílu vzduchu \(F_\mathrm{o}\). Velikost této síly závisí na rychlosti, a jak bude těleso zrychlovat, bude se zvětšovat i odporová síla. Protože odporová síla působí proti pohybu, respektive proti směru tíhové síly, bude se s jejím zvětšováním zmenšovat velikost zrychlení tělesa. Pohyb tedy sice bude stále zrychlený, ovšem nerovnoměrně a stále méně a méně; až se tyto dvě síly vyrovnají, zrychlení bude nulové, a pohyb se stane rovnoměrným. Těleso dosáhne své mezní rychlosti \(v_\mathrm{m}\), pro kterou platí \(F_\mathrm{O}=F_\mathrm{G}\) neboli \(\frac{1}{2}C\varrho Sv_\mathrm{m}^2=mg\).
Odtud pak můžeme mezní rychlost vyjádřit vztahem
\[v_\mathrm{m}=\sqrt{\frac{2mg}{C\varrho S}}\;.\]Nárůst odporové síly i rychlosti tělesa si můžete prohlédnout na následující animaci.
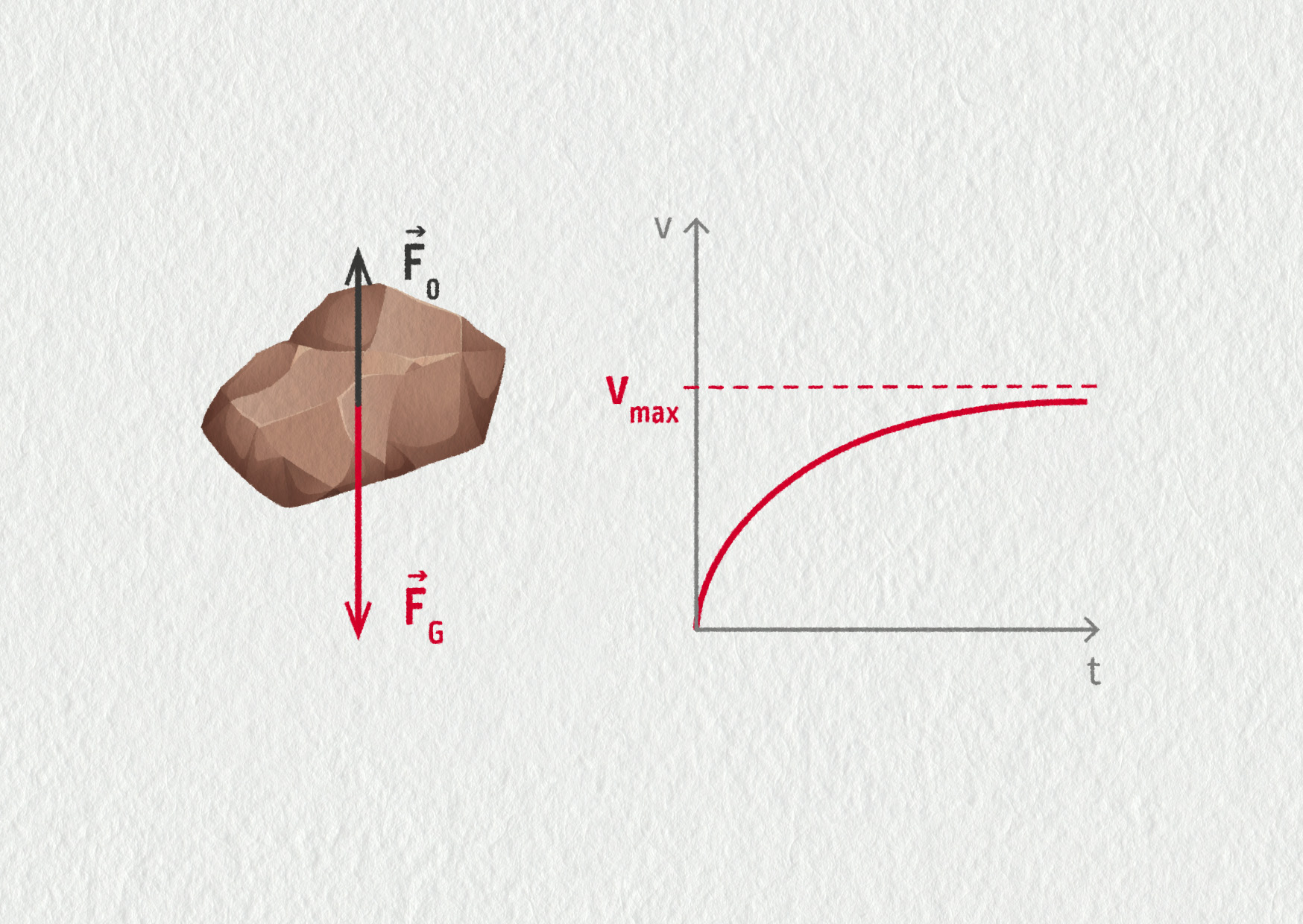
Zdroj
Úlohy, kde vystupují v čase proměnlivé síly, se řeší numerickými metodami (početními) nebo pomocí diferenciálních rovnic. Při numerickém řešení se snažíme postupovat krok po kroku. Vyjdeme z nějakých počátečních podmínek, například počáteční rychlost tělesa, a vypočítáme za pomoci druhého Newtonova zákona zrychlení tělesa v daném časovém okamžiku. Zvolíme malý časový krok, například Δt = 0,1 s, a určíme, o kolik se za tuto dobu změnila rychlost tělesa. Protože se změnila rychlost tělesa, změnila se i velikost odporové síly, a tím i hodnota zrychlení. Opět vypočítáme jeho hodnotu a opět vypočítáme novou hodnotu rychlosti o krok dt později. A tento postup stále opakujeme.
Numerické řešení na papíře je velmi pracné, pokud si ho však chcete vyzkoušet pomocí počítače a nasimulovat si různé druhy reálných pádů, podívejte se na podrobný návod v praktiku 15. kapitoly.
Budete si moci například vypočítat, s jakou rychlostí dopadne penny z Empire State Building nebo jiné podobné úlohy.
Video 5.46b – Simulace pádu s odporovou silou.
Vypočítejte maximální rychlost pádu dešťové kapky kulovitého tvaru o průměru 2 mm.
Kapka, a pro jednoduchost předpokládejme, že je kulovitého tvaru, dosáhne maximální rychlosti v okamžiku, kdy se obě působící síly, tedy tíhová a odpor vzduchu, vyrovnají. Jejich výslednice bude nulová a kapka se bude dále pohybovat pohybem rovnoměrným. Podle Newtonova vztahu pro velikost odporové síly je její velikost úměrná druhé mocnině rychlosti. Platí vztah \(F_\mathrm{O}=\frac{1}{2}C\varrho_\mathrm{vz}Sv^2\), kde \(C=0{,}45\) je hodnota součinitele odporu koule, \(\varrho_\mathrm{vz}=1{,}2\ \mathrm{kg/m}^3\) je hustota vzduchu, \(S=\pi r^2\) je obsah příčného průřezu kapky, pro výslednou rychlost pak dostáváme
\[v_\mathrm{m}=2\sqrt{\frac{2\varrho gr}{3C\varrho_\mathrm{vz}}}\;,\]kde ϱ je hustota vody. Číselně pak rychlost nabývá hodnoty 3,84 m/s, což odpovídá našim zkušenostem. Vodní kapky tedy díky nezanedbatelné odporové síle vzduchu dopadají na zem s mezní rychlostí přibližně 4 m/s. Samozřejmě závisí na jejich velikosti.
Poznámka: Hezký článek o tvaru dešťových kapek naleznete na https://www.meteopress.cz/vysvetleni/jaky-tvar-ma-destova-kapka/.

